VIII. Movimentação e Armazenagem
Introdução
O texto começa por fazer uma comparação dos custos de armazenagem com os custos logísticos de uma empresa, mostrando que a armazenagem tem um peso elevado nesses custos.
Dá a conhecer as maiores áreas cobertas de armazenagem no mundo, destacando a UPS e Wal Mart, no Brasil e o maior e mais avançado centro de distribuição multimodal de resinas plásticas do mundo.
Depois, são dadas informações sobre: armazéns insufláveis; diversos tipos de empilhadoras e suas possibilidades de utilização; o maior fabricante mundial de empilhadoras; os lideres do mercado das empilhadoras no Brasil; e sobre paletes, dando a conhecer a variedade de dimensões que estas têm em diversos locais do mundo.
O texto define exactidão na expedição e no inventário, dando a conhecer alguns dos melhores índices nestas áreas; o impacto que um mau endereçamento dos produtos tem nos custos do armazém; e os benefícios de utilização de Warehouse Management Systems (WMS) (Ferrão, 2006).
Unidade Mantida em Armazém (SKU)
«SKU» é o acrónimo de Stock Keeping Unit e pronuncia-se skew ou S K U, um código ou referência de cada variante dos artigos mantidos em armazém.
Um SKU é um identificador usado pelos armazenistas para permitir o seguimento sistemático dos produtos oferecidos aos clientes. Cada SKU identifica uma variante de um artigo, conforme a sua apresentação, tamanho, cor e outras características. Cada armazém pode ter o seu método de atribuir os códigos, como base em políticas regionais ou nacionais de armazenagem de dados da empresa. O seguimento de um SKU é diferente dos outros métodos de seguimento de produtos que são controlados por um vasto conjunto de regras estabelecidas pelos fabricantes ou, possivelmente, por entidades reguladoras.
Por exemplo: uma bola tem a referência 1234, é embalada em caixas com 20 bolas e a caixa é marcada com a mesma referência 1234. A caixa é então colocada no armazém. A caixa é a unidade mantida em armazém (SKU), porque é item armazenado. Não obstante as referências serem intermutáveis, designando quer uma bola ou uma caixa de bolas, a caixa de bolas é a unidade armazenada. Se existirem bolas de três cores diferentes, cada uma terá um SKU diferente. Quando o produto é expedido, podem sair 50 caixas de bolas azuis, 100 caixas de bolas vermelhas e 70 caixas de bolas amarelas. Esta expedição diz-se ter sido de 220 caixas, de três SKU's. Isto permite ao armazenistas determinar, por exemplo, se as bolas vermelhas se estão a vender mais que as bolas azuis.
O acrónimo SKU tornou-se mais visível com o advento do comércio electrónico, apresentando o SKU dos produtos nas páginas da Web. Na Figura 8.1 mostra-se um exemplo (Pereira, L., 2006b).

(carregar com o cursor na figura para ver em tamanho grande)
Fonte: Santos Silva
Unidade de Carga
Uma unidade de carga (unit load) é um volume de produto acondicionado de modo a possibilitar a movimentação e armazenagem como uma única unidade, independentemente do número de itens individuais que o constituem.
São exemplos de unidades de carga (Glickman e Schemmel, 1997):
- Paletes
- Fardos
- Peças individuais
- Tabuleiros
- Barris e Bidões
- Caixas
- Contentores para Avião ou Navio
Existem diversos factores (Tabela 8.1) que podem afectar a facilidade de transporte ou manuseio de materiais como, por exemplo (Muther, 1978):
- Tamanho
- Densidade ou estado de agregação
- Forma do material
- Risco de danos no material, instalações e pessoas
- Condição do item
- Valor ou custo (Raramente usado)
| B. Densidade | C. Forma | D. Risco | E. Condição |
| --- | Muito plano e empilhável ou possível de guardar em conjuntos (folhas de papel ou metal) | --- | --- |
| Muito leve (folha de metal) | Fácil de empilhar ou guardar em conjuntos (blocos de papel, pratos) | Não susceptível sofrer ou causar qualquer tipo de dano (ferro velho) | --- |
| Leve (papel canelado) | Razoavelmente empilhável ou fácil de guardar em conjuntos (livros, chávenas) | Susceptível a pouquíssimos danos (blocos de aço) | --- |
| Razoavelmente sólido (bloco de madeira) | Basicamente regular ou algo irregular (sacos de cereais) | Levemente susceptível a danos (bloco de madeira) | Limpo, firme e estável (bloco de madeira) |
| Razoavelmente pesado e denso (macho de fundição) | Comprido, arredondado ou algo irregular (sacos de grão e barras curtas) | Susceptível a danos produzidos por esmagamento, fracturas ou arranhões (obras de arte) | Oleoso, fraco, instável ou de difícil manuseio (aparas de madeira ou metal oleosas) |
| Pesado e denso (peça forjada) | Muito grande, esférico ou irregular (mesas) | Bastante susceptível a danos (ecrãs de televisão) | Coberto com lubrificante, quente, muito delicado ou escorregadio e de manuseio muito difícil |
| Muito pesado e denso (moldes, lingotes de chumbo) | Extremamente grande, curvo ou altamente irregular (vigas de aço) | Muito susceptível a danos (peças de cristal) | (superfícies pontiagudas) |
| --- | Extremamente grande e curvo ou extremamente irregular (tubos moldados, mobiliário) | Altamente susceptível a danos (ácido em garrafas, explosivos) | (aço fundido) |
(Pereira, L., 2006c).
Cross-Docking
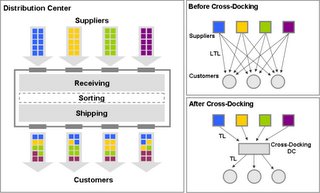
A técnica de cross-docking pode ser definida como uma operação de preparação de encomendas que não envolve o armazenamento dos produtos. A Wal-Mart foi pioneira na aplicação e desenvolvimento deste método (Chopra e Meindl, 2004).
Os camiões, vindos directamente dos fornecedores, cada um deles trazendo um tipo diferente de produto, entregam-nos numa instalação apropriada. Os produtos de cada camião são divididos em lotes mais pequenos e carregados noutros camiões que os transportam para a loja a que se destinam. A carga deste camiões é constituída por diferentes tipos e quantidades dos diversos produtos (Figura 8.2).
Fonte: Cross-Docking Distribution Center
Armazenagem Aleatória vs. Dedicada
Para ilustar o efeito do método de armazenagem nas necessidades de espaço, suponha-se que seis produtos são recebidos num armazém. As existências de cada um dos produtos no final de cada período são as apresentadas na Tabela 8.2. O valor agregado das existências obtém-se somando as existências dos seis produtos.
| Produtos | |||||||
| Período | 1 | 2 | 3 | 4 | 5 | 6 | Agregado |
| 1 | 24 | 12 | 2 | 14 | 11 | 12 | 73 |
| 2 | 22 | 9 | 8 | 8 | 10 | 9 | 66 |
| 3 | 20 | 6 | 6 | 4 | 9 | 6 | 51 |
| 4 | 18 | 3 | 4 | 24 | 8 | 3 | 60 |
| 5 | 16 | 36 | 2 | 20 | 7 | 24 | 105 |
| 6 | 14 | 33 | 8 | 16 | 6 | 21 | 98 |
| 7 | 12 | 30 | 6 | 12 | 5 | 18 | 83 |
| 8 | 10 | 27 | 4 | 8 | 4 | 15 | 68 |
| 9 | 8 | 24 | 2 | 4 | 3 | 12 | 53 |
| 10 | 6 | 21 | 8 | 24 | 2 | 9 | 70 |
| 11 | 4 | 18 | 6 | 20 | 1 | 6 | 55 |
| 12 | 2 | 15 | 4 | 16 | 24 | 3 | 64 |
| 13 | 24 | 12 | 2 | 12 | 23 | 24 | 97 |
| 14 | 22 | 9 | 8 | 8 | 22 | 21 | 90 |
| 15 | 20 | 6 | 6 | 4 | 21 | 13 | 70 |
| 16 | 13 | 3 | 4 | 24 | 20 | 15 | 79 |
| 17 | 16 | 36 | 2 | 20 | 19 | 12 | 105 |
| 18 | 14 | 33 | 8 | 16 | 13 | 9 | 93 |
| 19 | 12 | 30 | 6 | 12 | 17 | 6 | 83 |
| 20 | 10 | 27 | 4 | 8 | 16 | 3 | 68 |
| 21 | 8 | 24 | 2 | 4 | 15 | 24 | 77 |
| 22 | 6 | 21 | 8 | 24 | 14 | 21 | 94 |
| 23 | 4 | 18 | 6 | 20 | 13 | 18 | 79 |
| 24 | 2 | 15 | 4 | 16 | 12 | 15 | 64 |
| Soma dos níveis máximos de existências individuais Nível máximo do valor agregado das existências Nível médio do valor agregado das existências Nível mínimo do valor agregado das existências | = 140 = 105 = 77,5 = 51 | ||||||
Os níveis máximos das existências de cada um dos seis produtos são:
- Produto 1: 24
- Produto 2: 36
- Produto 3: 8
- Produto 4: 24
- Produto 5: 24
- Produto 6: 24
Dimensionamento de Armazém com Base nos Custos
Suponha-se que só se tem que armazenar um artigo. Defina-se um horizonte de planeamento T = 10 períodos de tempo. O custo fixo actualizado por unidade de capacidade de armazagem que se possui, durante o horizonte de planeamento, C0, é de 20 UM. O valor presente do custo de posse por unidade armazenada no espaço que se possui por período de tempo, C1, é de 1 UM e num espaço alugado, C2, é de 4 UM. As necessidades de espaço, ao longo do horizonte de planeamento, são: 4, 6, 8, 10, 9, 8, 7, 6, 5, e 4 para os períodos de tempo 1 a 10, respectivamente.
As procuras por período e por ordem decrescente, as respectivas frequências e soma cumulativa parcial das frequências estão representadas na Tabela 8.3. C' = C0 / (C2 - C1) = 20 / (4 - 1) = 6,7 e a soma cumulativa parcial das frequências excede 6,7 para uma procura de 6 unidades.
| Procura ordenada | Frequência | Soma parcial |
|---|---|---|
| 10 | 1 | 1 < 6,7 |
| 9 | 1 | 2 < 6,7 |
| 8 | 2 | 4 < 6,7 |
| 7 | 1 | 5 < 6,7 |
| 6 | 2 | 7 > 6,7 |
| 5 | 1 | 8 > 6,7 |
| 4 | 2 | 10 > 6,7 |
A capacidade óptima do armazém é, portanto, de 6 unidades. O custo total resultante é:
20 × 6 + 2 × 4 + 5 + 2 × 6 + (6 + 4) + 2 × (6 + 2 × 4) + (6 + 3 × 4) + (6 + 4 × 4) = 223 UM.
Se a capacidade for de 5 unidades o custo total é de 224 UM e se a capacidade for de 7 unidades o custo total é de 228 UM.
Suponha-se agora um horizonte de planeamento T = 50, com C0 = 100 UM, C1 = 4 UM e C2 = 8 UM. As necessidades de espaço são dadas na Tabela 8.4.
| Períodos | Espaço necessário | Períodos | Espaço necessário |
|---|---|---|---|
| - paletes - | - paletes - | ||
| 1-5 | 100 | 26-30 | 120 |
| 6-10 | 120 | 31-35 | 115 |
| 11-15 | 125 | 36-40 | 110 |
| 16-20 | 130 | 41-45 | 105 |
| 21-25 | 125 | 46-50 | 100 |
Neste caso C' = 100 / (8 - 4) = 25. Na Tabela 8.5, a soma parcial é igual a 25 quando a procura é igual a 120. Dado que a soma parcial é igual a C', há múltiplas soluções óptimas, nomeadamente, 115 ≤ Q ≤ 120 (Francis, et al, 1992 e Pereira, L., 2006l).
| Procura ordenada | Frequência | Soma parcial |
|---|---|---|
| 130 | 5 | 5 < 25 |
| 125 | 10 | 15 < 25 |
| 120 | 10 | 25 = 25 |
| 115 | 5 | 30 > 25 |
| 110 | 5 | 35 > 25 |
Planeamento do Layout de Armazém
As distâncias podem ser minimizadas guardando os artigos em áreas de armazenagem em profundidade e posicionando os materiais de forma a minimizar a distância total percorrida. Conforme é ilustrado na Figura 8.3, armazenando os artigos em áreas de armazenagem em profundidade, a distância percorrida será menor do que se os materiais forem armazenados em áreas sem profundidade.

(carregar com o cursor na figura para ver em tamanho grande)
A centralização das operações de recepção e expedição, também tem influência nos custos de operação do armazém, como se pode observar na Figura 8.4 (Tompkins e White, 1984 e Pereira, L., 2006h).

Figura 8.4. Impacte da centralização da recepção/expedição
conjugada com a armazenagem dedicada por classes
(carregar com o cursor na figura para ver em tamanho grande)
Afectação de Produtos a Locais de Armazenagem Dedicada
A configuração óptima dos produtos em armazenagem dedicada envolve a afectação dos produtos aos locais de armazenagem. As distâncias rectilineares são consideradas apropriadas e é usada a seguinte notação:
| q | = | número de locais de armazenagem |
| n | = | número de produtos |
| m | = | número de locais de entrada/saída (cais e/ou portas) |
| Sj | = | número de locais de armazenagem necessários para o produto j |
| Tj | = | número de entradas e saídas do armazém do produto j, isto é, as movimentações do produto j |
| pi | = | percentagem das entradas/saídas do armazém pelo ponto de entrada/saída i |
| dik | = | distância (ou tempo) que é necessário percorrer do ponto i ao local de armazenagem k |
| xjk | = | 1 se o produto j é afectado ao local de armazenagem k; caso contrário, 0 |
| f(x) | = | distância (ou tempo) média percorrida |
O problema do layout do armazém pode ser formulado da seguinte forma:
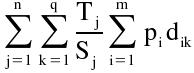
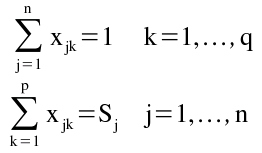
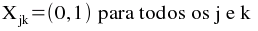 Supõe-se que cada artigo tem igual probabilidade de se movimentar entre o ponto de entrada/saída ou porta i e qualquer local de armazenagem afectado ao artigo j. Portanto, o valor de (1 / Sj) é a probabilidade de um local de armazenagem em particular afectado ao produto j ser escolhido para a movimentação de saída/entrada por uma porta. Fazendo
Supõe-se que cada artigo tem igual probabilidade de se movimentar entre o ponto de entrada/saída ou porta i e qualquer local de armazenagem afectado ao artigo j. Portanto, o valor de (1 / Sj) é a probabilidade de um local de armazenagem em particular afectado ao produto j ser escolhido para a movimentação de saída/entrada por uma porta. Fazendo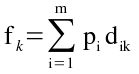 onde fk é a distância média percorrida entre o local de armazenagem k e as portas.
onde fk é a distância média percorrida entre o local de armazenagem k e as portas.Para minimizar a distância média total percorrida, procede-se do seguinte modo:
- Numerar os produtos de acordo com o valor de Tj / Sj, de forma que
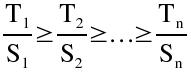
- Calcular os valores de fk para todos os locais de armazenagem.
- Afectar o produto 1 aos S1 locais de armazenagem que têm os menores valores de fk; afectar o produto 2 aos S2 locais de armazenagem que têm os menores valores de fk seguintes e assim sucessivamente (Pereira, L., 2006f).
Layout Óptimo com Armazenagem Dedicada
Considere-se um armazém cuja planta é ilustrada na Figura 8.5.
 Figura 8.5. Planta de um armazém
Figura 8.5. Planta de um armazémOs locais para armazenagem têm dimensões de 20 × 20 pés. As portas P1 e P2 são para camiões e as portas P3 e P4 são para vagões de caminho de ferro. É usada armazenagem dedicada. Sessenta por cento de todas as movimentações do armazém são feitas pelas portas P1 e P2, tendo cada porta a mesma probabilidade de ser usada. Quarenta por cento de todas as movimentações do armazém são divididas igualmente pelas portas P3 e P4.
Neste armazém vão ser armazenados três produtos, A, B e C, com um único tipo de produto armazenado no mesmo local. O produto A necessita de 3 600 pés2 de espaço de armazenagem e é movimentado à taxa de 750 unidades de carga por mês; o produto B necessita de 6 400 pés2 de espaço de armazenagem e é movimentado à taxa de 900 unidades de carga por mês; o produto C necessita de 4 000 pés2 e é movimentado à taxa de 800 unidades de carga por mês.
A distância apropriada é a rectilinear, medida entre as portas e os centróides dos locais de armazenagem. Os valores de fk (distância média do local de armazenagem k às portas) estão apresentados na Figura 8.6. Para exemplificar o cálculo de um fk, suponha-se que k = 29. Medindo as distâncias rectilineares do centróide do local de armazenagem 29 a cada uma das quatro portas tem-se d1, 29 = 120, d2, 29 = 100, d3, 29 = 100 e d4, 29 = 80. Então,
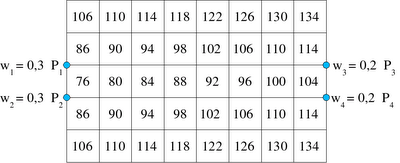 Figura 8.6. Distância média de cada local de armazenagem k às portas
Figura 8.6. Distância média de cada local de armazenagem k às portasO número de locais de armazenagem necessário para cada produto é SA = 3 600 / 400 = 9, SB = 16 e SC = 10. Os valores de Tj são TA = 750, TB = 900, TC = 800. Portanto, os valores de Tj / Sj são TA / SA = 83 1/3, TB / SB = 56,25 e TC / SC = 80. Então os produtos são numerados 1(A), 2(C) e 3(B).
O produto 1(A) necessita de 9 locais de armazenagem; então, os locais de armazenagem afectados ao produto A são [17, 18, 19, 9, 25, 20, 10, 26, 21]. O produto 2(C) necessita de 10 locais de armazenagem; então, [11, 27, 22, 12, 28, 23, 13, 29, 24, 1] são afectados ao produto C. O produto 3(B) necessita de 16 locais de armazenagem; então, o produto B é afectado aos locais de armazenagem [14, 30, 33, 2, 15, 31, 34, 3, 16, 32, 35, 4, 36, 5, 37, 6]. Os locais 7, 8, 38, 39 e 40 ficam disponíveis para armazenar equipamento, sanitários, escritórios e outros.
Um layout que minimiza a distância média percorrida por unidade de tempo é mostrado na Figura 8.7. É importante salientar que o layout apresentado não é o único que minimiza a distância média percorrida por unidade de tempo, nem necessariamente o layout final. Nada mais foi considerado, para além da distância média percorrida; a utilização desta abordagem da armazenagem dedicada deve ser examinada em cada aplicação em particular. No entanto, o layout serve de base para a avaliação de outras configurações (Pereira, L., 2006g).
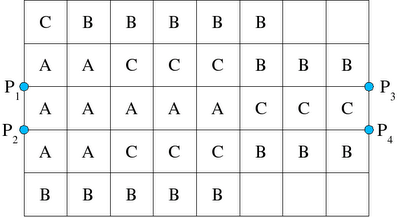 Figura 8.7. Layout que minimiza a distância média percorrida por unidade de tempo
Figura 8.7. Layout que minimiza a distância média percorrida por unidade de tempoConfiguração Contínua de Armazém
Em várias situações práticas o projecto de layout é para mum armazém já existente. Para ilustrar a abordagem seguida, considere-se um armazém com as dimensões 200 ft × 150 ft com uma única porta localizada como se mostra na Figura 8.8.
 Figura 8.8. Planta de armazém
Figura 8.8. Planta de armazémÉ utilizada armazenagem aleatória e o espaço necessário é de 18 000 ou 27 500 ft2. Supõe-se que a probabilidade da movimentação de um artigo entre a porta e qualquer ponto no espaço de armazenagem é a mesma e supõe-se que as deslocações são rectilineares.
Construindo curvas de nível dentro do armazém existente resulta em três famílias diferentes de formas geométricas, cono se mostra na Figura 8.9.
 Figura 8.9. Linhas de isocusto para um armazém existente
Figura 8.9. Linhas de isocusto para um armazém existenteA linha de isocusto de menor valor tem forma triangular e é aplicável a áreas que não excedam 10 000 ft2; o conjunto seguinte de linhas de isocusto aplica-de a áreas entre 10 000 ft2 e 20 000 ft2; e o último conjunto de linhas de isocusto aplica-se a áreas de armazenagem entre 20 000 ft2 e 30 000 ft2.
A área de armazenagem (A) delimitada por uma linha de isocusto pode ser expressa como uma função do valor da linha de isocusto (k) da seguinte forma:

No primeiro caso, a curva de nível tem forma triangular com uma base igual a 2 × k e uma altura de k; a área é k2 com valores de k a variarem de 0 a 100 ft enquanto a área interior varia de 0 a 10 000 ft2.
No segundo caso, começando no ponto onde a linha de isocusto intersecta a parede superior da instalação, a distância da linha de isocusto ao ponto de entrada / saída é a soma de 100 ft percorridos paralelamente ao eixo dos y's e (k - 100) ft percorridos paralelamente ao eixo dos x's. A linha de isocusto varia entre 100 e 150 ft à medida que a ára de armazenagem varia de 10 000 a 20 000 ft2. A forma geométrica da linha de isocusto pode ser representada como a união de um rectângulo de dimensões 200 ft × (k - 100) ft e um triângulo de 200 ft de base e 100 ft de altura. Assim, a área limitada pela linha de isocusto é 200 k - 10 000.
No terceiro caso, a área limitada pela linha de isocusto pode ser obtida simplesmente subtraindo a área exterior à linha de isocusto, da área total do edifício. Cada canto do edifício fora da linha de isocusto tem uma forma triangular de dimensões (250 - k) × (250 - k). Então, a área limitada pela linha de isocusto é igual à área do edifício, 30 000, menos a soma das áreas dos dois cantos, (250 - k)2. As linhas de isocusto variam entre valores de 150 a 250 ft enquanto a área de armazenagem varia de 20 000 a 30 000 ft2.
Fazendo A igual a 18 000 e resolvendo em ordem a k dá um valor de 140 ft (usando a equação A = 200 k - 10 000) e o resultado pode ser observado na Figura 8.10.
 Figura 8.10. Área de armazenagem de 18 000 ft2
Figura 8.10. Área de armazenagem de 18 000 ft2Fazendo A igual a 27 500 e resolvendo em ordem a k dá um valor de 200 ft [usando a equação A = 30 000 - (250 - k2)] e resulta na configuração que pode ser observada na Figura 8.11 (Francis, et al, 1992 e Pereira, L., 2006m).
 Figura 8.11. Área de armazenagem de 27 500 ft2
Figura 8.11. Área de armazenagem de 27 500 ft2Regiões de Armazenagem Dedicada para Dois Produtos
Considerem-se dois produtos, 1 e 2. As necessidades de espaço são, respectivamente, S1 = 2 500 ft2 e S2 = 2 400 ft2. As movimentações são, respectivamente, T1 = 100 e T2 = 50 por dia. T1 / S1 = 0,04 e T2 / S2 = 0,021. Como (T1 / S1) > (T2 / S2) o produto 1 é colocado no layout primeiro. Para delimitar a zona ocupada pelo produto 1 é necessário construir uma linha de isocusto que delimite a área de 2 500 ft2. Existe uma única porta, localizada ao longo do eixo y's e a região de armazenagem deve ocupar apenas o primeiro e quarto quadrantes. Então uma região de armazenagem triangular com 100 ft de base e 50 ft de profundidade ou altura é afectada ao produto 1. A união das duas áreas de armazenagem é também limitada por uma linha de isocusto triangular. Como as duas áreas combinadas somam 4 900 ft2, esta área deve ser limitada por uma linha de isocusto triangular com 140 ft de base e 70 ft de altura, como se mostra na Figura 8.12 (Pereira, L., 2006n).
 Figura 8.12. Áreas de armazenagem de produtos com uma única porta
Figura 8.12. Áreas de armazenagem de produtos com uma única portaNo caso de locais de armazenagem discretos, a distância média percorrida, dentro da zona de armazenagem, pode ser determinada somando as distâncias médias de cada produto. Esta distância pode ser determinada somando as distâncias percorridas de e para todos os locais de armazenagem afectados a um produto, dividindo a soma pelo número de locais afectados ao produto e multiplicando o resultado pelo número médio de movimentações efectuadas por período de tempo, pelo produto. De forma semelhante, no caso de armazenagem contínua, a distância média, para uma região de armazenagem dedicada a um produto, pode ser obtida integrando a região de armazenagem e multiplicando o resultádo pela razão entre o número de movimentações e o espaço afectado ao produto.
Em alternativa à integração sobre toda a região, é possível integrar ao longo das linhas de isocusto que definem a região. Para fazer isso, é necessário desenvolver uma relação funcional entre o valor de uma linha de isocusto e a área que envolve. Para facilitar a descrição da abordagem da «integração pela linha de isocusto», considere-se a Figura 8.13, envolvendo a utilização de armazenagem aleatória.
 Figura 8.13. Layout de armazenagem contínua
Figura 8.13. Layout de armazenagem contínuaA região de armazenagem é servida por um única porta, localizada na origem; a região de armazenagem está contida no primeiro e quarto quadrantes; supõe-se que as movimentações são rectilineares.
Como se mostra na Figura 8.13, a linha de isocusto resultante é um triângulo. Escolhendo uma linha de isocusto arbitrária qualquer de valor k, a área envolvida (A) é igual a k2. Portanto,
A = k2 = q (k)
q (k) é a relação funcional entre A e k; especificamente, é a área de um conjunto de nívelde valor k. Mais ainda, invertendo a equação anterior,
k = A½ = r (A)
r (A) é a função inversa que relaciona k com A e determina-se resolvendo q (k) em ordem a k. A função inversa de r (t) pode ser calculada a partir de A = q (r (t)). Por exemplo, q (k) = k2 resulta em A = r (A)2 ou r (A) = A½.
Geralmente, à medida que uma linha de isocusto varia do valor mínimo ao máximo, a área envolvida varia do valor mínimo ao valor A. Neste caso, o valor mínimo da linha de isocusto pode ser obtido a partir da equação anterior, fazendo A igual a zero; o valor máximo pode ser obtido igualando a mesma equação à área de armazenagem a envolver.
No exemplo da Figura 8.13 a área limitada é de 152 000 ft2. Aplicando a equação k = A½ = r (A), o valor mínimo da linha de isocusto é zero e o valor máximo é 389,8717 ft. Para calcular a distância média percorrida, pode-se usar a seguinte expressão com um integral simples:
 onde E[R] é a distância média percorrida na região de armazenagem R, T é o número de «viagens» de e para o armazém por unidade de tempo (i.e., as movimentações), f (X) é a distância média por viagem de ou para o ponto X, e q' (k) é a primeira derivada de q (k) em ordem a k.
onde E[R] é a distância média percorrida na região de armazenagem R, T é o número de «viagens» de e para o armazém por unidade de tempo (i.e., as movimentações), f (X) é a distância média por viagem de ou para o ponto X, e q' (k) é a primeira derivada de q (k) em ordem a k.Para explicar a equação anterior, note-se que a função distrubição para a distância percorrida é dada por q (k) / A; portanto a função densidade é dada por q' (k) / A para r (0) ≤ k ≤ r (A). Portanto a distância média percorrida é como indicado acima.
Para ilustrar o uso da equação anterior no cálculo da distância média percorrida, considere o exemplo da Figura 8.13. Aplicando a equação anterioir temos:
 Portanto, para a movimentação de uma unidade por minuto e uma área de 152 000 ft2, E[R] = 259,9145 ft/min (Pereira, L., 2006o).
Portanto, para a movimentação de uma unidade por minuto e uma área de 152 000 ft2, E[R] = 259,9145 ft/min (Pereira, L., 2006o).Considere-se o exemplo anterior com dois produtos, 1 e 2. As necessidades de espaço são, respectivamente, S1 = 2 500 ft2 e S2 = 2 400 ft2. As movimentações são, respectivamente, T1 = 100 e T2 = 50 por dia. As áreas de armazenagem dos dois produtos num espaço com uma única porta são ilustradas na Figura 8.14.
 Figura 8.14. Armazenagem de dois produtos numa área com uma única porta
Figura 8.14. Armazenagem de dois produtos numa área com uma única portaPor extensão dos resultados para um único produto, a distância média percorrida é dada por
 onde T1 e T2 são os valores das movimentações dos produtos 1 e 2, respectivamente.
onde T1 e T2 são os valores das movimentações dos produtos 1 e 2, respectivamente.Os limites do segundo integral resultam da linha de isocusto que limita a região do produto 2 tomar os valores expressos em termos da área total de armazenagem envolvida. Desta forma, as linhas de contorno para o produto 2 variam em valor desde o máximo para o produto 1 até um valor que coincide com a envolvente das áreas conjuntas dos dois produtos. Assim sendo,
 (Pereira, L., 2006p).
(Pereira, L., 2006p).Suponha-se que a região de armazenagem se localiza no primeiro e quarto quadrantes, duas portas (P1 e P2) se localizam ao longo do eixo dos y's separadas pela distância c, a movimentação rectilinear de/para o armazém tem igual probabilidade de ocorrência para cada porta e é necessária uma área de armazenagem A.
Na Figura 8.15, r é a distância rectilinear desde a intersecção da linha de isocusto com o eixo dos y's à porta mais próxima. A linha de isocusto envolve uma área de
A = r (c + r)
A linha de contorno é um trapézio cuja área é dada por
A = h × (a + b) / 2
onde a é o comprimento da base menor, b o comprimento da base maior e h a altura do trapézio. Assim, a área limitada pela linha de isocusto da Figura 8.15 pode ser expressa como
r × (c + 2 × r + c) / 2 = r (c + r)
Resolvendo em ordem a r tem-se
0,5 [(4 A + c2)½ - c]
Se um peso de 0,5 for associado a cada porta, a relação entre r e k, o valor da linha de isocusto, é dada por
k = 0,5 r + 0,5 (r + c )
ou
r = k - 0,5 c
 Figura 8.15. Região de armazenagem contínua com duas portas
Figura 8.15. Região de armazenagem contínua com duas portasSubstituindo r, na primeira equação, pelo valor de r dado pela última equação, obtém-se
A = (k - 0,5 c) × (k + 0,5 c)
ou
A = k2 - 0,25 c2 = q (k)
Para além disso, resolvendo para k como uma função de A,
k = (A + 0,25 c2)½ = r (A)
e
r (0) = 0,5 c
A distância média percorrida é dada por
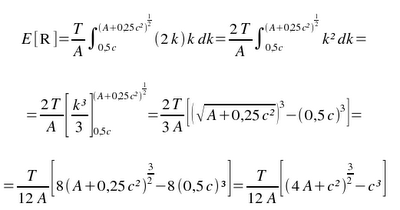
Suponha-se que a área de armazenagem delimitada pela linha de isocusto tem 10 000 ft2, que as portas estão separadas por uma distância de 20 ft e são feitas 100 operações de entrada / saída por hora. Para c = 20 ft, T = 100 por hora e A = 10 000 ft2, E [R] = 6 760,25 ft/hora (Pereira, L., 2006q).
Considere-se o exemplo anterior, mas com várias classes de produtos. Então para o produto j:
q (kj) = kj2 - 0,25 c2
r (Bj) = (Bj + 0,25 c2)½
onde Bj = A1 + ... + Aj. Para o caso de três classes de produtos, a distância média percorrida é dada por
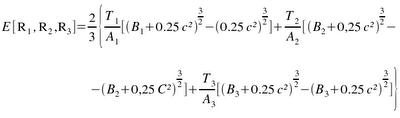
Suponha-se são feitas 100 movimentações por hora e que o espaço total necessário são 10 000 ft2. Os produtos da Classe I representam 75% das movimentações e 15% das necessidades de espaço; os produtos da Classe II representam 20% das movimentações e 35% do espaço de armazenagem; e os produtos da classe II representam 5% das movimentações e 50% do espaço. Fazendo T1 = 75, A1 = 1 500, T2 = 20, A2 = 3 500, T3 = 5 e A3 = 5 000, as razões entre as movimentações e os espaços para as três classes de produtos são 0,05, 0,0057 e 0,001. Com c = 20 ft, a distância média percorrida para as três classes é de 3 677,49 ft/hora.
Para estabelecer um limite superior para o espaço necessário em armazenagem aleatória resultar na mesma distância média percorrida em armazenagem dedicada das três classes de produtos, faz-se a distância média percorrida por uma classe de produtos de área desconhecida igual à distância média percorrida pelas três classes de produtos. Então, da última equação da entrada anterior, com c = 20 ft, T = 100 por hora e E [R] = 3 677,49 ft/hr,
100 [(4 Ars + 202)½ - 203] / (12 Ars) = 3 677,49
Resolvendo em ordem a Ars por métodos numéricos resulta um valor aproximado de 2 771,86 ft2. Portanto, com base nos resultados obtidos, para um armazém com duas portas do mesmo lado e três classes de produtos com as razões entre as movimentações e o espaço dadas, em comparação com os 10 000 ft2 para a armazenagem dedicada, o espaço necessário para a armazenagem aleatória não pode exceder 27,72% da área do sistema de armazenagem dedicada para se obter o mesmo valor para a distância média percorrida (Pereira, L., 2006r).


0 Comments:
Post a Comment
<< Home