VIII. Movimentação e Armazenagem (Continuação)

Armazenagem por Empilhamento

O empilhamento envolve o armazenamento de unidades de carga em pilhas nas filas de armazenagem. Utiliza-se, frequentemente, quando se tem que armazenar grandes quantidades de alguns produtos e estes podem ser empilhados até uma altura razoável sem esmagamento da carga. É muito utilizado para alimentos, bebidas, electrodomésticos e produtos de papel entre outros. A utilização de espaço é grande, com um baixo investimento (Tompkins, 1996).

Durante o ciclo de armazenagem e retirada de um lote de produto, podem ocorrer vagas numa fila de armazenagem. Para se conseguir uma rotação FIFO dos lotes, os locais de armazenagem vagos não podem ser utilizados para a armazenagem de outros produtos ou lotes até que todas as cargas tenham sido retiradas da fila.

O projecto de uma armazenagem por empilhamento é caracterizado pela: profundidade de fila de armazenagem (x), o numero de filas de armazenagem necessárias para um dado lote de produto (y) e a altura da pilha (z), onde as variáveis de decisão, x, y e z têm que ter valores inteiros. Se a altura da pilha é fixa, então a variável de decisão mais importante é a profundidade da fila de armazenagem.

Considere-se a seguinte notação:

S = quantidade média de área no chão necessária durante a permanência de um lote no armazém;
S_BS = quantidade média de área no chão necessária, com empilhamento e sem stock de segurança;
Q = tamanho do lote a armazenar, em unidades de carga;
W = largura de uma unidade de carga;
L = altura ou profundidade de uma unidade de carga;
c = afastamento lateral entre unidades de carga;
A = largura do corredor de armazenagem;
x = profundidade de uma fila de armazenagem, em unidades de carga;
z = altura da pilha, em unidades de carga ou níveis de armazenagem;
y = número de filas de armazenagem necessárias para conterem Q unidades de carga com empilhamento;
η = número médio de filas de armazenagem necessárias durante a permanência de um lote no armazém, com empilhamento.

Para desenvolver um modelo para calcular a quantidade média de área no chão necessária, com empilhamento e sem stock de segurança, note-se que essa quantidade média é igual à área ocupada no chão por uma fila de armazenagem (incluindo metade do corredor e do afastamento lateral) vezes a número médio de filas de armazenagem necessárias durante a permanência de um lote de um produto no armazém. Então,

S_BS = η (W + c) (x L + 0,5 A),

com:

η = y (2 Q - x y z + x z) / 2 Q.

Substituindo η na equação de S_BS, vem:

S_BS = y (W + c) (x L + 0,5 A) (2 Q - x y z + x z) / 2 Q.

Como S_BS não é uma função convexa de x, para determinar o mínimo é necessário enumerar S_BS, em função de x. Note-se que o valor óptimo não depende de W ou c (Alesly, 2006a).

Suponha-se que L = 48", W = 50", A = 144", c = 10", z = 4 e Q = 200. Qual é o valor de x que minimiza S_BS?

Enumerando S_BS (3.ª coluna da Tabela 8.6), em função de x (1.ª coluna da Tabela 8.6) e ordenando S_BS (6.ª coluna da Tabela 8.6), obtém-se o valor de x = 10, para um mínimo de S_BS = 99 360 polegadas² ou 64,1 m². Os valores de y (2.ª e 5.ª colunas da Tabela 8.6) são calculados atendendo a que x y z ≥ Q (Alesly, 2006b).

Tabela 8.6. Valor de x que minimiza S_BS.

x	y	SBS		x	y	SBS
		(polegadas²)				(polegadas²)
50	1	148 320,0		10	5	99 360,0
49	2	148 348,8		8	7	99 590,4
48	2	148 262,4		9	6	99 792,0
47	2	148 060,8		7	8	99 878,4
46	2	147 744,0		11	58	100 800,0
45	2	147 312,0		12	5	101 088,0
44	2	146 764,8		6	9	101 088,0
43	2	146 102,4		13	4	101 894,4
42	2	145 324,8		5	10	102 960,0
41	2	144 432,0		14	4	103 564,8
40	2	143 424,0		15	4	104 544,0
39	2	142 300,8		16	4	104 832,0
38	2	141 062,4		17	3	105 494,4
37	2	139 708,8		4	13	107 078,4
36	2	138 240,0		18	3	107 827,2
35	2	136 656,0		19	3	109 814,4
34	2	134 956,8		20	3	111 456,0
33	2	133 142,4		21	3	112 752,0
32	2	131 212,8		22	3	113 702,4
31	2	129 168,0		23	3	114 307,2
30	2	127 008,0		25	2	114 480,0
29	2	124 732,8		24	3	114 566,4
28	2	122 342,4		3	17	114 566,4
27	2	119 836,8		26	2	117 216,0
26	2	117 216,0		27	2	119 836,8
25	2	114480,0		28	2	122 342,4
24	3	114 566,4		29	2	124 732,8
23	3	114 307,2		30	2	127 008,0
22	3	113 702,4		31	2	129 168,0
21	3	112 752,0		2	25	131 040,0
20	3	111 456,0		32	2	131 212,8
19	3	109 814,4		33	2	133 142,4
18	3	107 827,2		34	2	134 956,8
17	3	105 494,4		35	2	136 656,0
16	4	104 832,0		36	2	138 240,0
15	4	104 544,0		37	2	139 708,8
14	4	103 564,8		38	2	141 062,4
13	4	101 894,4		39	2	142 300,8
12	5	101 088,0		40	2	143 424,0
11	5	100 800,0		41	2	144 432,0
10	5	99 360,0		42	2	145 324,8
9	6	99 792,0		43	2	146 102,4
8	7	99 590,4		44	2	146 764,8
7	8	99 878,4		45	2	147 312,0
6	9	101 088,0		46	2	147 744,0
5	10	102 960,0		47	2	148 060,8
4	13	107 078,4		48	2	148 262,4
3	17	114 566,4		50	1	148 320,0
2	25	131 040,0		49	2	148 348,8
1	50	183 600,0		1	50	183 600,0

Aproximação Contínua

Para valores grandes de Q, pode usar-se uma aproximação contínua de S_BS fazendo Q = x y z . Substituindo y por Q / x z e x y z por Q, tem-se:

S_BS^c = (W + c) (x L + 0,5 A) (Q + x z) / 2 x z,

Derivando S_BS^c em relação a x, igualando o resultado a zero e resolvendo em ordem a x, obtém-se a aproximação contínua do valor óptimo de x:

x_BS^c = [A Q / 2 L z]^½.

Para o exemplo anterior:

x_BS^c = 8,66.

Uma aproximação ao valor óptimo de x é 8 ou 9, a 2.^a e 3.^a melhores soluções do problema, com mais, respectivamente, 0,2 e 0,4 % de área média que a solução óptima.

Estes resultados, tal como se pode observar nas tabelas, mostram que os valores da área média óptima não são muito sensíveis aos valores de x e que, talvez com mais interesse, os valores óptimos de x não são particularmente sensíveis a alterações no valor de Q (Alesly, 2006e).

Armazenagem por Empilhamento com Stock de Segurança

O modelo de armazenagem por empilhamento pode ser modificado para incluir o stock de segurança (s) identificando as condições em que se verifica. O stock de segurança para um determinado produto é criado recebendo um lote de substituição antes de se esgotarem as existências desse produto. Então um stock de segurança implica que, de um lote que acabou de chegar, não vai ser retirada nenhuma palete durante algum tempo. Neste caso, o número médio de filas de armazenagem é:

η = y [2 (Q + s) - x y z + x z] / 2 (Q + s).

Então, a área média necessária durante a existência de um lote com stock de segurança S_BSSS é dada por:

S_BSSS = y (W + c) (x L + 0,5 A) [2 (Q + s) - x y z + x z] / 2 (Q + s).

Note-se que o denominador é o dobro do tempo de ciclo e não duas vezes o tamanho do lote.

Para o exemplo anterior, com s = 10, na 6.ª coluna da Tabela 8.7 obtém-se o valor de x = 10, para um mínimo de S_BSSS = 102 514 polegadas² ou 66,1 m² (Alesly, 2006c).

Tabela 8.7. Valor de x que minimiza S_BSSS.

x	y	SBSSS		x	y	SBSSS
		(polegadas²)				(polegadas²)
50	1	148 320,0		10	5	102 514,3
49	2	155 136,0		9	6	103 680,0
48	2	154 779,4		8	7	103 968,0
47	2	154 313,1		7	8	104 448,0
46	2	153 737,1		11	5	104 571,4
45	2	153 051,4		13	4	104 996,6
44	2	152 256,0		12	5	105 531,4
43	2	151 350,9		6	9	105 531,4
42	2	150 336,0		5	10	106 971,4
41	2	149 211,4		14	4	107 136,0
40	2	147 977,1		17	3	108 082,3
39	2	146 633,1		15	4	108 617,1
38	2	145 179,4		16	4	109 440,0
37	2	143 616,0		18	3	110 715,4
36	2	141 942,9		4	13	111 785.1
35	2	140 160,0		19	3	113 019,4
34	2	138 267,4		20	3	114 994,3
33	2	136 265,1		25	2	116 297,1
32	2	134 153,1		21	3	116 640,0
31	2	131 931,4		22	3	117 956,6
30	2	129 600,0		23	3	118 944,0
29	2	127 158.9		26	2	119 177,1
28	2	124 608,0		24	3	119 602,3
27	2	121 947,4		3	17	109 602,3
26	2	119 177,1		27	2	121 947,4
25	2	116 297,1		28	2	124 608,0
24	3	119 602,3		29	2	127 158,9
23	3	118 944,0		30	2	129 600,0
22	3	117 956,6		31	2	131 931,4
21	3	116 640,0		32	2	134 153,1
20	3	114 994,3		32	2	136 265,1
19	3	113 019,4		2	25	136 800,0
18	3	110 715,4		34	2	138 267,4
17	3	108 082,3		35	2	140 160,0
16	4	109 440,0		36	2	141 942,9
15	4	108 617,1		37	2	143 616,0
14	4	107 136,0		38	2	145 179,4
13	4	104 996,6		39	2	146 633,1
12	5	105 531,4		40	2	147 977,1
11	5	104 571,4		50	1	148 320,0
10	5	102 514,3		41	2	149 211,4
9	6	103 680,0		42	2	150 336,0
8	7	103 968,0		43	2	151 350,9
7	8	104 448,0		44	2	152 256,0
6	9	105 531,4		45	2	153 051,4
5	10	106 971,4		46	2	153 737,1
4	13	111 785,1		47	2	154 313,1
3	17	119 602,3		48	2	154 779,4
2	25	136 800,0		49	2	155 136,0
1	50	192 000,0		1	50	192 000,0

Aproximação Contínua

Uma aproximação contínua da situação com stock de segurança obtém-se substituindo, igualmente, y por Q / x z e x y z por Q, na equação de S_BSSS. As expressões resultantes para a quantidade média de espaço e da profundidade óptima da fila são:

S_BSSS^c = Q (W + c) (x L + 0,5 A) (Q + 2 s + x z) / 2 (Q + s) x z.

e

x_BSSS^c = [(A (Q + 2 s) / 2 L z)]^½.

Para o exemplo acima, com s = 10:

x_BS^c = 9,08.

Uma aproximação ao valor óptimo de x é 9 ou 10, respectivamente a 2.^a melhor e a solução óptima do problema, com uma diferença de 1,1 % de área média, em relação à solução óptima (Alesly, 2006e).


Armazenagem em Profundidade

A armazenagem em profundidade é muito parecida com a armazenagem por empilhamento, mas cada unidade de carga não se apoia em nenhuma outra. Por isso, não há perdas de espaço vertical. A entrada e saída das unidades de carga é feita pelo mesmo lado da fila, com uma sequência LIFO. É um tipo de armazenagem com uma elevada densidade, apropriado para armazenar grandes quantidades. Podem ser armazenadas dez ou mais unidades de carga numa única fila, com as unidades de carga umas atrás das outras.

Como cada fila de armazenagem é independente de todas as outras, tanto horizontal como verticalmente, a área afecta a uma fila é inversamente proporcional à altura da armazenagem. Então, a quantidade média de área no chão necessária, com armazenagem em profundidade e stock de segurança é dada por:

S_DLSS = ξ (W + 2 c + r) [x L + 0,5 (A + f)] / z,

onde

ξ = número médio de filas de armazenagem em profundidade necessárias durante a permanência de um lote no armazém;
r = largura da prumada das estantes;
f = profundidade do espaço de ventilação entre as traseiras das filas de armazenagem;

com

ξ = υ [2 (Q) + s) - x υ + x] / 2 (Q + s),

onde

υ = número de filas de armazenagem em profundidade necessárias para Q unidades de carga.

Substituindo υ na equação de S_DLSS, vem:

S_DLSS = υ (W + 2 c + r) [x L + 0,5 (A + f)] [2 (Q + s) -

- x υ + x] / 2 (Q + s) z.

Para o exemplo anterior, com r = 3" e f = 6", na 6.ª coluna da Tabela 8.8 obtém-se o valor de x = 20, para um mínimo de S_DLSS = 107 936 polegadas² ou 69,6 m². Os valores de υ (2.ª e 5.ª colunas da Tabela 8.8) são calculados atendendo a que υ é o menor inteiro maior ou igual a Q / x z (Alesly, 2006d).

Tabela 8.8. Valor de x que minimiza S_DLSS.

x	υ	SDLSS		x	υ	SDLSS
		(polegadas²)				(polegadas²)
1	200	236 233,2		20	10	107 935,7
2	100	164 953,9		17	12	108 250,1
3	67	141 542,0		19	11	108 505,4
4	50	129 940,0		16	13	108 572,4
5	40	123 187,5		25	8	108 587,5
6	34	119 056.2		18	12	108 696,0
7	29	116 011,6		21	10	108 706,1
8	25	113 684,5		23	9	108 813,3
9	23	112 487,0		15	14	108 815,6
10	20	110 933,9		14	15	109 062,0
11	19	110 519,1		22	10	109 101,1
12	17	109 642,4		13	16	109 343,6
13	16	109 343,6		24	9	109 404,6
14	15	109 062,0		26	8	109 465,2
15	14	108 815,6		12	17	109 642,4
16	13	108 572,4		29	7	109 768,3
17	12	108 250,1		27	8	110 091,3
18	12	108 696,0		28	8	110 492,8
19	11	108 505,4		11	19	110 519,1
20	10	107 935,7		30	7	110 595,0
21	10	108 706,1		10	20	110 933,9
22	10	109 101,1		31	7	111 246,5
23	9	108 813,3		34	6	111 259,8
24	9	109 404,6		32	7	111 722,9
25	8	108 587,5		33	7	112 024,0
26	8	109 456,2		35	6	112 100,6
27	8	110 091,3		9	23	112 487,0
28	8	110 492,8		40	5	112 693,8
29	7	109 768,3		36	6	112 816,3
30	7	110 595,0		37	6	113 406,8
31	7	111 246,5		41	5	113 629,7
32	7	111 722,9		8	25	113 684,5
33	7	112 024,0		38	6	113 872,2
34	6	111 259,8		39	6	114 212,4
35	6	112 100,6		42	5	114 482,3
36	6	112 816,3		43	5	115 251,4
37	6	113 406,8		44	5	115 937,0
38	6	113 872,2		7	29	116 011,6
39	6	114 212,4		50	4	116 148,2
40	5	112 693,8		45	5	116 539,3
41	5	113 629,7		46	5	117 058,1
42	5	114 482,3		51	4	117 085,2
43	5	115 251,4		47	5	117 493,5
44	5	115 937,0		48	5	117 845,5
45	5	116 539,3		52	4	117 972,2
46	5	117 058,1		49	5	118 114,0
47	5	117 493,5		53	4	118 809,1
48	5	117 845,5		6	34	119 056,2
49	5	118 114,0		54	4	119 595,9
50	4	116 148,2		55	4	120 332,7
...	...	...		...	...	...

Aproximação Contínua

A aproximação contínua para a armazenagem em profundidade com stock de segurança é dada pela expressão:

S_DLSS^c = Q (W + 2 c + r) [x L + 0,5 (A + f)] (Q + 2 s + x) / 2 (Q + s) z x

e

x_DLSS^c = [(A + f) (Q + 2 s) / 2 L]^½

Para o exemplo anterior:

x_DLSS^c = 18,54

Uma aproximação ao valor óptimo de x é 18 ou 19, a 6.^a e 3.^a melhores soluções do problema, com mais, respectivamente, 0,7 e 0,5 % de área média que a solução óptima (Alesly, 2006e).


Estantes para Paletes

As estantes para paletes de profundidade simples e dupla podem ser consideradas casos especiais de armazenamento em profundidade com x = 1 e x = 2, respectivamente.


Estantes para Paletes de Profundidade Dupla
A largura da vista de cima de uma estante para paletes de profundidade dupla é

W + 1,5 c + 0,5 r

A profundidade da vista de cima de uma estante para paletes de profundidade dupla é

2 L + 0,5 (A + f)

A área afecta a um lugar de armazenagem de profundidade dupla é, novamente, inversamente proporcional à altura da armazenagem. Então, a quantidade média de área no chão necessária, com armazenagem de profundidade dupla e stock de segurança, é dada por

S_DDSS = υ (W + 1,5 c + 0,5 r) [2 L + 0,5 (A + f)] [2 (Q + s) – 2 υ) + 2] / 2 (Q + s) z

e sem stock de segurança

S_DD = υ (W + 1,5 c + 0,5 r) [2 L + 0,5 (A + f)] (Q - υ + 1) / Q z

Uma vez que profundidade de armazenagem é conhecida, υ é igual a Q / 2, se Q é par, e (Q + 1) / 2, se Q é ímpar.

Então, se Q é par, tem-se

S_DDSS = Q (W + 1,5 c + 0,5 r) [2 L + 0,5 (A + f)] (Q + 2 s + 2 ) / 4 (Q + s) z

e

S_DD = (W + 1,5 c + 0,5 r) [2 L + 0,5 (A + f)] (Q + 2) / 4 z

e, se Q é ímpar, então

S_DDSS = (Q + 1) (W + 1,5 c + 0,5 r) [2 L - 0,5 (A + f)] (Q + 2 s) + 1) / 4 (Q + s) z

e

S_DD = (W + 1,5 c + 0,5 r) [2 L + 0,5 (A + f)] (Q + 1)² / 4 Q z

Para o exemplo anterior, com s = 10, atendendo a que Q = 200, então υ = 100 e o valor óptimo de S_DDSS = 150 266,3 polegadas² ou 96,9 m² e, sem stock de segurança, S_DD = 143 565,2 polegadas² ou 92,6 m².


Estantes para Paletes de Profundidade Simples
Para determinar a quantidade média de área no chão necessária em armazéns com estantes para paletes de profundidade simples, a profundidade da vista de cima é igual a

L + 0,5 (A + f)

A largura é a mesma que para a estante de profundidade dupla. Com x = 1 e υ = Q, fazendo a modificação apropriada nas equações para o armazenamento em profundidade, a quantidade média de área no chão necessária para estantes para paletes de profundidade simples, com stock de segurança, é dada por

S_SDSS = Q (W + 1,5 c + 0,5 r) [L + 0,5 (A + f)] (Q + 2 s + 1) / 2 (Q + s) z

Na ausência de stock de segurança, a equação anterior reduz-se a

S_SD = (W + 1,5 c + 0,5 r) [L + 0,5 (A + f)] (Q + 1) / 2 z

Para o mesmo exemplo, υ = 200, S_SDSS = 215 198,8 polegadas² ou 138,8 m² e, sem stock de segurança, S_SD = 205 509,9 polegadas² ou 132,6 m² (Alesly, 2006f).


Sistemas de armazenagem automática (AS/RS)


Estimativa dos custos de um
sistema de armazenamento automático (AS/RS)
Para desenvolver uma base para estimar o custo do investimento num sistema de armazenamento automático, Zollinger (1982) compilou informações detalhadas sobre mais de 60 sistemas de armazenamento automático. A estimativa do investimento obtém-se somando: o custo das prateleiras, incluindo instalação e carris de suporte das empilhadoras; equipamento de armazenagem, incluindo controlos, electrificação, carris de guia e instalação; e o custo do edifício de construção convencional, incluindo serviços e aspersores (Tompkins e White, 1984).

Representando por x o volume de uma unidade de carga, em pés cúbicos, y o peso da unidade de carga e z a altura das prateleiras medida em unidades de carga, tem-se a seguinte estimativa para o custo por lugar de armazenagem nas prateleiras.

Custo por lugar nas prateleiras [US(1982)$] = 25 (0,924 84 + 0,025 x + 0,000 442 4 y – (y² / 82 500 000) + 0,233 28 z – 0,004 76 z²)

Segundo Tompkins et al. (1996), a actualização do custo por lugar nas prateleiras pode ser feita por estimativa do primeiro factor, US(1982)$25, na equação acima. Substituindo pelo parâmetro α, em UM, fica então:

Custo por lugar nas prateleiras [UM] = α (0,924 84 + 0,025 x + 0,000 442 4 y – (y² / 82 500 000) + 0,233 28 z – 0,004 76 z²)

Supondo que uma unidade de carga de 2 000 lb ocupa 53,2 pés3 e vão ser armazenadas dez unidades de carga verticalmente, então o custo por lugar nas prateleiras é de

US(1982)$25 [0,924 84 + 0,25 (53,2) + 0,000 442 4 (2 000) – (2 000² / 85 500 000) + 0,233 28 (10) – 0,004 76 (10)²] = US(1982)$123,70 por lugar.

Para fins de planeamento, é usado um custo de US(1982)$125 por lugar de armazenagem nas prateleiras (Alesly, 2006g).

Para determinar o custo da máquina de armazenagem, Zollinger (1982) considera três factores: a altura do AS/RS, o peso da unidade de carga e o tipo e localização do sistema de controlo. Se a altura do AS/RS for inferior a 11 m, então aplica-se um custo base de US(1982)$21 000 por máquina de armazenagem; se o AS/RS tem entre 11 e 15 m, então adiciona-se um custo de US(1982)$21 000 a cada máquina de armazenagem; para alturas acima dos 15 e até 23 m, adiciona-se um custo de US(1982)$42 000 ao custo base de cada máquina de armazenagem; para alturas de 23 a 34 m, incorre-se num custo incremental de US(1982)$63 000 (acima do custo base); e para alturas acima dos 34 m, adiciona-se um custo incremental de US(1982)$84 000.

Se a carga pesa menos que 0,5 t, então a contribuição para o custo é de US(1982)$21 000 por máquina de armazenagem; para pesos entre 0,5 e 1,5 t, a contribuição para o custo é de US(1982)$42 000 por máquina de armazenagem; para cargas pesando entre 1,5 e 3 t, a contribuição para o custo é de US(1982)$63 000 por máquina de armazenagem; e para cargas acoma das 3 t, adicionam-se US(1982)$84 000 ao custo total de cada máquina de armazenagem.

Se o sistema de controlo é só manual, incorre-se num custo de US(1982)$21 000$ por máquina de armazenagem; se o sistema de controlo se localiza a bordo, a contribuição para o custo de cada máquina de armazenagem é de US(1982)$42 000; se o sistema de controlo se localiza fora da máquina, a contribuição para o custo é de US(1982)$63 000 por máquina de armazenagem; e se for usado um sistema central para controlar todas as máquinas de armazenagem, a contribuição para o custo é de US(1982)$84 000 por cada máquina de armazenagem.

Como a relação entre todos os custos e o custo base é linear, a actualização do custo da máquina de armazenagem pode ser feita por estimativa de parâmetros correpondentes aos custos base em relação à altura, peso da carga e tipo de controlo.

Suponha-se que o AS/RS vai ter 17 m de altura, movimentar cargas de 900 Kg e um sistema de controlo centralizado. O custo por máquina de armazenagem é determinado como se segue (Alesly, 2006h):

Factor	Valor	Custo
		-- US(1982)$ --
Altura	17 m	21 000 + 42 000
Peso	0,9 t	42 000
Controlo	Centralizado	84 000
Custo /	máquina de armazenagem	189 000

Zollinger (1982) detectou que o preço do edifício variava com a altura do edifício. A tabela seguinte mostra os factores de conversão para determinar o custo por m² para várias alturas do edifício; um edifício de 7,6 m serve como ponto base.

Pé Direito	Factor de Conversão
- m -
7,6	1,00
12,2	1,25
16,8	1,50
21,3	1,90
25,9	2,50

Suponha-se que se quer construir um espaço de armazenagem de 43 608 m³. Um edifício de 16,8 m deve ter uma área de 2 596 m² a um custo de 1,5 (2 596) c ou 3 894 c, onde c é o custo por m² para um edifício de 7,6 m de altura. Se for construído um edifício de 7,6 m de altura, é necessária uma área de 5 738 m² e o custo é de 5 738 c. De igual modo, se for construído um edifício de 21,3 m de altura, o custo é, aproximadamente, 3 890 c. Um edifício de 25,9 m de altura custa aproximadamente 4 209 c. Então, um edifício de 21,3 m de altura é a solução óptima em termos de custo do edifício (Alesly, 2006i).

Suponha-se que todas as unidades de carga a armazenar num sistema de armazenagem automático são do mesmo tamanho e têm o mesmo peso. Represente-se por x a profundidade, y a largura e z a altura de uma unidade de carga. Considere-se que as prateleiras de um AS/RS têm n níveis de armazenagem de altura e m colunas de armazenagem de comprimento. Considere-se, ainda, que um corredor de AS/RS inclui o espaço de armazenagem de ambos os lados do corredor, em prateleiras de profundidade simples. Então a altura (H), comprimento (L) e largura (W) de um corredor de AS/RS, são dadas por:

H [cm] = n (z + 25)

L [cm] = m (y + 20)

W [cm] = 3 (x + 15) (com aspersores entre as estantes)
ou
W [cm] = 3 (x + 10) (sem aspersores entre as estantes)

Atendendo a que o nível inferior de armazenagem não pode ficar ao nível do chão e o tecto não é colocado directamente sobre o nível superior de armazenagem, supôe-se que o primeiro espaço está a 71 cm acima do chão e o tecto está a 51 cm acima do nível superior de armazenagem. Então, a altura do edifício será H + 122 cm.

Para determinar o comprimento do edifício, Zollinger (1982) indica uma estimativa do espaço necessário para os postos de levantamento e depósito (P/D), extensão do S/R ou excesso para além do fim das prateleiras e corredor para transportador ou empilhadora. O comprimento adicional depende da largura da palete, como se mostra na tabela seguinte:

	Comprimento	Adicional
Largura da Palete	sem Carros de Tranferência	com Carros de Tranferência
-------------------------- m ---------------------------
0,76	7,93	12,80
0,91	8,84	13,72
1,02	9,14	14,33
1,07	9,45	14,63
1,22	10,36	15,85
1,32	10,97	16,46

A largura do edifício é obtida multiplicando a largura de um corredor de armazenagem, W, pelo número de corredores de armazenagem. Ao produto devem ser adicionados 61 cm para levar em conta o espaço entre as paredes e as estantantes.


Suponha-se que um AS/RS está a ser projectado para unidades de carga de 1,02 × 1,22 m com 1,22 m de altura. Vai haver oito corredores; cada corredor tem 12 unidades de carga de altura e 80 de comprimento. Vão ser usados aspersores entre as estantes e não haverá carros de transferência.

A altura do edifício será 12 (122 + 25) + 120 = 1 884 cm. É, então, necessário um edifício de 19 m de altura. O comprimento do edifício é de 80 (122 + 20) + 1 036 cm, ou seja, 124 m. A largura do edifício é de 8 × 3 (102 + 15) + 61 cm, ou seja, 29 m.

Dependendo das outras funções que forem localizadas nestas instalações e a quantidade de espaço necessário para preparação ou acumulação de unidades de carga na «frente» do AS/RS, pode ser necessário um edifício maior (Alesly, 2006j).


Tempo de ciclo da máquina de S/R
A máquina de S/R de carga unitária desloca-se no corredor simultaneamente na horizontal e vertical. Então, o tempo necessário para se deslocar dos postos de P/D para um local de armazenagem é o máximo dos tempos de deslocamento na horizontal e vertical.

Por causa da importância do tempo de ciclo no desenvolvimento da capacidade do sistema, dá-se uma atenção especial ao tempo que a máquina de S/R leva a executar ambos os ciclos de comando simples e comando duplo. Um ciclo de comando simples consiste numa armazenagem ou numa retirada do armazém, mas não ambas; enquanto um ciclo de comando duplo envolve tanto uma armazenagem como uma retirada.

Para determinar os tempos de ciclo (p. 30) supõe-se que um ciclo de armazenamento de comando simples começa com a S/R no posto de P/D, levanta uma carga, desloca-se para o local de armazenamento, deposita a carga e regressa vazia ao posto de P/D. Um ciclo de comando simples de retirada de uma carga do armazém é também suposto começar com a S/R no posto de P/D, de onde se desloca vazia para o local de retirada da carga, levanta a carga, desloca-se para o posto de P/D e deposita a carga.

Um ciclo de comando duplo é suposto começar com a S/R no posto de P/D; levanta uma carga, desloca-se para o local de armazenamento, deposita a carga, desloca-se vazia para o local de retirada da carga, levanta a carga, desloca-se para o posto de P/D e deposita a carga. Com um ciclo de comando duplo são feitos um total de dois levantamentos e dois depósitos.

Supondo armazenagem aleatória, um posto de P/D num extremo do corredor localizado na base da estante, velocidades horizontal e vertical constantes e locais de armazenagem nas estantes de tamanho único, os tempos de ciclo são:

T_SC = T(1 + Q² / 3) + 2 T_P/D

T_DC = T / 30 (40 + 15 Q² – Q³) + 4 T_P/D

onde

T = max (t_h, t_v)

Q = min (t_h / t_v, t_v / t_h)

com

T_SC = tempo de ciclo de comando simples
T_DC = tempo do ciclo de comando duplo
T_P/D = tempo para fazer um levantamento ou um depósito
t_h = tempo necessário para a deslocação horizontal do posto de P/D para o local
mais distante do corredor
t_v = tempo necessário para a deslocação vertical do posto de P/D para o local mais distante do corredor

Para determinar os tempos de ciclo para operações de comando simples e duplo para o sistema de estantes dimensionado anteriormente (Sistemas de armazenagem automática (AS/RS) (IV)), suponha-se que a S/R necessita de 0,35 min para executar uma operação de P/D, desloca-se horizontalmente a uma velocidade média de 6,4 km/h e desloca-se verticalmente a uma velocidade média de 1,1 km/h.

As dimensões (em metros) da estante são 1,42 m (comprimento) por 1,47 n (altura), onde m é o número de endereços na horizontal e n é o número de endereços na vertical. Neste caso, m = 80 e n = 12. As distâncias de deslocação na horizontal e vertical são, portanto:

d_h = 1,42 x 80 = 113,79 m

d_v = 1,47 x 12 = 17,68 m

Supõe-se que a máquina de S/R se desloca no máximo 113,79 m na horizontal e 17,68 m na vertical. Na realidade, o mecanismo de vai-vem tem que ser elevado só até à posição de apoio da carga no décimo segundo nível de armazenagem, em vez de até ao cimo da estante. A distância percorrida na horizontal está, provavelmente, subestimada de 0,61 a 3,05 m, conforme a localização do posto de P/D.

Os tempos máximos de deslocação horizontal e vertical são determinados como se segue:

t_h = d_h / V_h = 113,792 / (6,4 x 1 000 / 60) = 1,07 min

t_v = d_v / V_v = 17,68 / (1,1 x 1 000 / 60) = 0,97 min

Então,

T = max (1,07, 0,97)

T = 1,07

e

Q = 0,97 / 1,07 = 0,9

Portanto, os tempos de ciclo de comando simples e comando duplo são:

T_SC = T(1 + Q² / 3) + 2 T_P/D

= 1,07 [1 + 0,9² / 3] + 2 x 0,35 = 2,06 min por ciclo de comamdo simples

T_DC = T / 30 (40 + 15 Q² – Q³) + 4 T_P/D

= 1,07 / 30 (40 + 15 x 0,9² – 0,9³) + 4 x 0,35 = 3,23 min por ciclo de comamdo duplo

Então, o tempo médio de ciclo por operação é 2,06 min com um ciclo de comando simples e 1,62 min com um ciclo de comando duplo (Alesly, 2006k).


Utilização da máquina de S/R

Para a situação considerada anteriormente, suponha-se que 40% das entradas e saídas do armazém são realizadas como operações de comando simples e as restantes são executadas como operações de comando duplo. Com o AS/RS devem ser feitas 120 entradas e outras tantas saídas do armazém por hora.

Suponha-se que não se tem carros de transferência e que as 8 máquinas de S/R são carregadas uniformemente. Então cada S/R deve executar 15 armazenagens por hora e 15 retiradas por hora. Dado que 6 entradas e 6 saídas do armazém por hora são realizadas usando uma operação de comando simples (isto é, 40%), há 9 operações de comando duplo por hora. A carga de trabalho da máquina de S/R obtém-se da seguinte forma:

Carga de trabalho / S/R = 2 × 6 × 2,06 + 9 × 3,23 = 53,79 min/h

Portanto, cada S/R é utilizada 53,79 / 60, ou 89,65%. O ciclo médio por operação é de 53,79 / 30 ou 1,79 min por operação.

Dado que o tempo entre os pedidos de armazenagem e/ou retirada de cargas do armazém são variáveis aleatórias e uma vez que as localizações dos endereços de armazenamento e/ou retirada de cargas do armazém a serem visitados num ciclo de comando simples ou duplo são variáveis aleatórias, pode usar-se a análise de filas de espera para ajudar no projecto de um AS/RS. Contudo, devido à mistura de operações de comando simples e duplo e a distribuição de probabilidades genérica dos tempos de deslocação, sugere-se uma abordagem por simulação.

Os carros de transferências são utilizados quando o nível de actividade num corredor não é suficiente para justificar a utilização de uma máquina AS/RS para cada corredor. Para determinar o templo de ciclo para um AS/RS com carro de transferência, o tempo necessário para efectuar a transferência tem que ser incluído. Para além disso, podem ocorrer interferências entre as S/R quando várias máquinas de S/R estão servidas por um único carro de transferência. Por causa da rede de filas envolvidas no projecto de AS/RS com carros de transferência, é geralmente usada a análise por simulação para ajudar na determinação do número de máquinas S/R e disciplinas de operação associadas (Alesly, 2006u).


Projecto de AS/RS

1. Determinar o tamanho, configuração e peso das unidades de carga

O projecto e configuração de um sistema de S/R automático envolve duas características físicas determinantes. A primeira é o tamanho e configuração das cargas. Isto determina o espaço tridimensional necessário para armazenar cada unidade de material. O material ou unidade de carga pode ser uma simples palete ou contentor. Ou podem ser rolos e varões de metal ou madeira, rolos de carpetes ou grandes electrodomésticos. Qualquer que seja a unidade de carga, deve-se determinar o menor espaço em que, na prática, possa ser armazenada, por ser determinante para o dimensionamento do espaço de armazenagem individual necessário. Dado que o tamanho de unidade de carga pode variar, na configuração final pode ser necessário mais do que um tamanho de espaço de armazenagem. Pequenas variações no tamanho dos espaços de armazenagem não são, contudo, significativas para fins orçamentais. Para este exercício orçamental basta determinar as dimensões máximas das cargas (Harnischfeger, s.d.).

Dimensões máxima da carga:

Comprimento (profundidade) _____ Largura _____ Altura ______

Juntamente com o tamanho máximo da carga, determina-se a orientação de carga relativamente às prateleiras de armazenagem para determinar a largura do espaço de armazenagem. Se a carga é paletizada, por exemplo, a carga é orientada com as longarinas da palete paralelas ao corredor da grua empilhadora para tirar partido da capacidade máxima da palete.

Largura do espaço de armazenamento necessária _______________

O peso da unidade de carga é a segunda característica física que tem que ser considerado, atendendo a que afecta o projecto estrutural das estantes de armazenagem. Basta determinar o peso máximo das unidades de carga que vão ser movimentadas (Alesly, 2006l).

Peso máximo da unidade de carga individual __________________


2. Determinar quantos locais de armazenagem são necessários

A quantidade máxima de existências de unidade de carga que se deseja armazenar em qualquer momento determina o número total de locais de armazenagem que o sistema deve ter. O número total de unidades de carga, é claro que é constituído, muito provavelmente, por vários tipos diferentes de existências.

A determinação do número máximo de unidades de carga necessárias em armazém deve basear-se nas operações actuais, mais uma estimativa razoável das necessidades futuras. Geralmente, do planeamento inicial até à operacionalidade completa de um sistema automático de armazenagem, vão até dois anos, por isso devem-se estimar as necessidades de armazenagem para pelo menos dois anos mais tarde (Alesly, 2006m).

Número de locais de armazenagem necessários ________________


3. Determinar a utilização de sistema: quantas cargas necessitam de entrar e sair do sistema, por hora

A actividade de movimentação está directamente relacionmada com as acividades de produção e expedição. É, simplesmente, uma questão de determinar quantas unidades de carga é necessário armazenar e quantas é necessário retirar em cada hora de funcionamento. Não se deve calcular a média horária durante um turno qualquer. É preciso saber as taxas horárias máximas a que as cargas entram e saem para se manter todas as instalações a funcionar eficientemente (Alesly, 2006n).

Número máximo de cargas a armazenar / hr __________________

Número máximo de cargas a retirar do armazém / hr ___________

Picos invulgares nas necessidades de entradas e saídas por hora, se alguns _________________________


4. Determinar o número de gruas e estantes necessárias no sistema

Os requisitos de utilização do sistema determinam quantas e que tipos de gruas de armazenamento e retirada de cargas do armazém são necessárias, em termos de gruas de ciclo simples ou duplo por hora.

Como já se viu (Tempo de ciclo da máquina de S/R) a operação de ciclo duplo significa que uma grua, começando no posto de levantamento, executa consecutivamente um comando de armazenagem e retirada de cargas do armazém. Uma grua pode realizar 22 ciclos duplos por hora, o que representa a entrada de 22 cargas e saída de 22 cargas por hora.

A operação de ciclo simples significa que uma grua, começando no posto de levantamento, executa um comando de armazenagem ou de retirada de carga do armazém e aguarda o comando seguinte nessa posição. Uma grua pode realizar 32 ciclos simples por hora, o que representa uma combinação qualquer de 32 cargas entradas ou retiradas do armazém por hora.

De uma maneira geral, deve-se planear para gruas de ciclo duplo para se ter o factor de eficiência mais elevado - duas cargas por ciclo.

Se a velocidade de entrada ou saída é crítica, deve-se, todavia, considerar a operação mais rápida dos ciclos simples. Por exemplo, o funcionamento das instalações podem determinar que alguns turnos sejam dedicados inteiramente à armazenagem ou à retirada de cargas do armazém. Isto pode ocorrer se se produz e armazena toda a produção num turno e depois se tem uma pequena equipa, no segundo turno, para retirar todo o produto para expedição.

Em quaisquer instalações em que diversos componentes têm que interagir para executar uma única função, surgem ineficiências que impedem um componente do sistema de operar a 100% da capacidade. Simulações realizadas em computador e a experiência indicam que o projecto de um AS/RS deve basear-se numa grua a trabalhar a 85% da capacidade teórica máxima.

Para determinar o número de gruas necessárias, usa-se uma das seguintes fórmulas:

A. Grua de ciclo duplo

utilização (do passo 3) / (22 [ciclos duplos / hora] × 0,85 ) = Número de gruas necessárias _____________

B. Grua de ciclo simples

utilização (do passo 3) / (32 [ciclos simples / hora] × 0,85 ) = Número de gruas necessárias ____________


Estantes no sistema

Uma grua pode servir para vários corredores ou ser dedicada a um dado corredor. Num sistema de uma grua por corredor, por exemplo, uma grua serve duas estantes. Portanto, para determinar o número de estantes no sistema, multiplica-se o número de gruas por dois (Alesly, 2006o).

Número de gruas × 2 = _______________ estantes.


5. Determinar a altura do sistema em unidades de carga

Geralmente, a altura de um sistema varia entre 9 a 27 m (30 a 90 pés), dependendo da altura da carga e número de cargas em altura. A altura para os sistemas mais eficientes é de 15 a 21 m (50 a 70 pés).

Para determinar a altura total do sistema de, determina-se, primeiro, a altura da carga de acordo com a Figura 8.16. O exemplo mostra uma carga paletizada ou contentor cúbico de 1,2 m (4 pés). A altura da carga consiste na soma da altura real da carga mais a altura necessária para os elementos da estante que suportam a carga e a entrada do vai-vem da grua (Figura 8.16). Para cargas até 1,1 t (2 500 libras) (carga leve), esta altura adicional deve ser de 15 cm (6 polegadas). Para cargas acima de 1,1 t (2 500 libras) (carga pesada), esta altura adicional deve ser de 23 cm (9 polegadas).


Figura 8.16.
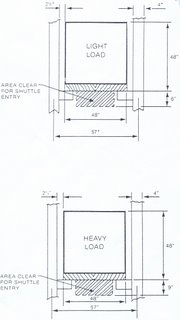
(carregar com o cursor na figura para ver em tamanho grande)

Dividindo a altura da carga pela altura mínima de 15 m (50 pés) ou altura máxima de 21 m (70 pés) de um sistema e subtraindo um, determina-se o número de cargas em altura do sistema. Subtrai-se uma carga para levar em conta as distâncias necessárias ao tecto e ao chão (Figura 8.17). Em ambos os casos a altura do sistema está dentro dos parâmetros recomendados. Geralmente, o valor mais alto, no exemplo, é o mais eficiente a comprar.

Figura 8.17.
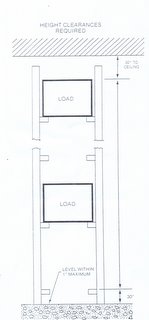
(carregar com o cursor na figura para ver em tamanho grande)

Exemplo:

15 / (1,2 + 0,15) altura de uma carga leve = 11 - 1 = 10 cargas de altura

[50 pés / (4 pés + 6 polegadas)]

21 / (1,2 + 0,15) altura de uma carga leve = 15 - 1 = 14 cargas de altura

[(70 pés / (4 pés + 6 polegadas)]


Novo cálculo:

A. 15 / altura da carga em m (altura real mais adicional) =
[50 / altura da carga em pés (altura real mais adicional)] =

= número mínimo de cargas __________ menos 1 = ____________

B. 21 / altura da carga em m (altura real mais adicional) =
[70 / altura da carga em pés (altura real mais adicional)] =

= número mínimo de cargas __________ menos 1 = ____________


Nos passos seguintes supõe-se que o número de cargas em altura (determinado acima) é o maior valor calculado (Alesly, 2006p).


6. Determinar o número de colunas necessário

Utilizar a seguinte fórmula:

Número de unidades de carga que é necessário armazenar / (2 × número de gruas × número de unidades de carga em altura)

No passo 2, determinou-se o número de unidades de carga que é necessário armazenar.

No passo 4, determinou-se o número de gruas necessárias e este número é idêntico ao número mínimo de corredores necessários no sistema. o número mínimo de corredores multiplicado por dois, é igual ao número mínimo de estantes num sistema (há uma estante de cada lado de cada corredor).

No passo 5, determinou-se o número de unidades de carga em altura.

Então, basta preencher com os dados e fazer as contas (Alesly, 2006q).


Exemplo:

10 000 unidades de carga que é necessário armazenar / ( 2 × 5 gruas × 14 unidades de carga em altura) = 72 colunas


Novo cálculo:

______ unidades de carga que é necessário armazenar / (2 × ______ gruas × ______ unidades de carga em altura) = ______ colunas


7. Determinar o comprimento do sistema

Primeiro determina-se o comprimento das prateleiras do sistema, que consiste no número total de colunas numa fila. Isto é feito determinando a largura da coluna, como mostra na Figura 8.16 do passo 5 e multiplicando pelo número de colunas. Para calcular a largura de uma coluna, adiciona-se a folga lateral da carga mais a largura de um pilar da estante à largura da carga.

Exemplo:

1,37 m (4,5 pés) largura de colunas × 72 colunas = 98,76 m (324 pés) comprimento da estante do sistema de armazenagem

Idealmente, o comprimento destas estantes de armazenagem deve estar entre estantes estariam entre 76,2 e 121,9 m (250 e 400 pés) para maximizar a eficiência da grua.


Novo cálculo:

______ m largura da colunas × ______ colunas = ______ m comprimento da estante do sistema de armazenagem

Uma vês que estes cálculos só levam em conta o comprimentos da estante de armazenagem, têm que se fazer algumas adições para se obter o comprimento total do sistema.

Para a movimentação da grua e postos de levantamento e depósito (Figura 8.18), adicione-se 7,62 m (25 pés).


Figura 8.18.
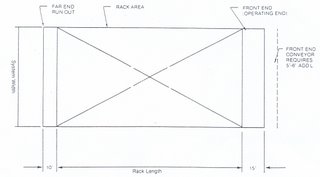
(carregar com o cursor na figura para ver em tamanho grande)

Se o sistema necessitar também de outros equipamentos para movimentação das cargas, tais como correias transportadoras, sistemas puxados por cabo, veículos sem condutor ou carro de transferência, deve-se levar em conta o comprimento adicional que necessita de ser somado para obter o comprimento total do sistema (Alesly, 2006r).


Novo cálculo:

______ m comprimento da estante do sistema de armazenagem
+ 7,62 m movimentação da grua e postos de levantamento e depósito
+_____ m valor adicional para equipamentos especiais =
______ m comprimento total do sistema

[______ pés comprimento da estante do sistema de armazenagem
+ 25 pés movimentação da grua e postos de levantamento e depósito
+_____ pés valor adicional para equipamentos especiais =
______ pés comprimento total do sistema]


8. Determinar a largura do sistema

Para determinar a largura, deve-se definir a unidade de corredor. Uma unidade de corredor é a largura total de um corredor e das estantes de armazenagem adjacentes.

A unidade de corredor é determinada multiplicando a profundidade máxima de uma unidade de carga por três a adicionando 61 cm (2 pés) para as folgas entre entre estantes e corredor. Multiplicando a unidade de corredor pelo número de corredores determina-se a largura do sistema (Alesly, 2006s).

Para um sistema com 5 corredores (passo 4) calcule-se como se segue:

Exemplo:

Profundidade (largura) de uma carga (1,22 m) × 3 + 0,61 m = 4,27 m por unidade de corredor
[Profundidade (largura) de uma carga (4 pés) × 3 + 2 pés = 14 pés por unidade de corredor]

4,27 m (unidade de corredor) × 5 (corredores) = 21,34 m
[14 pés (unidade de corredor) × 5 (corredores) = 70 pés]

Novo cálculo:

Profundidade (largura) de uma carga ______ m × 3 + 0,61 m = ______ m por unidade de corredor

______ m (unidade de corredor) × ______ (número de corredores) = ______ m largura do sistema

[Profundidade (largura) de uma carga ______ pés × 3 + 2 pés = ______ pés por unidade de corredor

______ pés (unidade de corredor) × ______ (número corredores) = ______ pés largura do sistema]


Tipos de layouts alternativos para um dado conjunto de parâmetros

Quaisquer que sejam os parâmetros básicos, a configuração do sistema pode variar alterando algumas das variáveis, tais como o número de cargasa em altura ou o número de colunas. Seguem-se alguns exemplos:

Parâmetros:

Palete de 1,07 × 1,22 m, com 1,22 m de altura, cargas de 900 a 1 800 kg.
[Palete de 42 × 48 polegadas, com 48 polegadas de altura, cargas de 2 000 a 4 000 libras].
Movimentações de 85 a 100 ciclos duplos / hora
(requer um mínimo de 5 gruas e 5 corredores).
Necessidade de armazenar 10 000 cargas ± 1%.


Configuração do Sistema # 1

Altura de 10 cargas × 100 colunas × 10 estantes de armazenagem = 10 000 cargas.

Dimensões do sistema:

Altura de 16,76 m de altura × [129,54 m de comprimento + 7,62 m (espaço à frente e ao fundo)] × 21,34 m de largura.
{Altura de 55 pés × [425 pés de comprimento + 25 pés (espaço à frente e ao fundo)] × 70 pés de largura}.


Configuração do Sistema # 2

Altura de 12 cargas × 84 colunas × 10 estantes de armazenagem = 10 080 cargas.

Dimensões do sistema:

Altura de 18,59 m de altura × [108,81 m de comprimento + 7,62 m (espaço à frente e ao fundo)] × 21,34 m de largura.
{Altura de 61,75 pés × [357 pés de comprimento + 25 pés (espaço à frente e ao fundo)] × 70 pés de largura}.


Configuração do Sistema # 3

Altura de 14 cargas × 72 colunas × 10 estantes de armazenagem = 10 080 cargas.

Dimensões do sistema:

Altura de 21,64 m de altura × [93,27 m de comprimento + 7,62 m (espaço à frente e ao fundo)] × 21,34 m de largura.
{Altura de 71,25 pés × [306 pés de comprimento + 25 pés (espaço à frente e ao fundo)] × 70 pés de largura} (Alesly, 2006v).


A. Opções do sistema para reduzir custos

Os cálculos precedentes estabeleceram os parâmetros e orçamentos para um sistema de armazenagem automático com base nas necessidades usuais. Contudo, há opções no projecto dos sistemas que podem reduzir os custos da maquinaria e cotroladores necessários. Aqui estão dois exemplos:

1. Sistema com carros de transferência de corredor

Uma necessidade de armazenar um grande número de unidades de carga juntamente com uma taxa de movimentações baixa pode sugerir a utilização de um sistema de carro de transferência das gruas que permita que as gruas no sistema sirvam vários corredores. A experiência com este sistema dita que um carro de transferência geralmente trabalha com uma grua e que a transferência da grua entre corredores ocorre pouco frequentemente, de modo a maximizar a utilização da grua. Deve haver uma relação de, pelo menos, três corredores por grua, para que se possa considerar a ideia do carro de transferência como uma alternativa viável à abordagem de uma grua por corredor. Adicionalmente, é preciso contabilizar, uns 6 m (20 pés) adicionais de comprimento do sistema para o carro de transferência.

2. Armazenagem em estantes de profundidade dupla

A armazenagem de cargas em profundidade dupla, ou armazenagem das cargas uma atrás de outra em locais de armazenagem de dupla profundidade, pode ser uma boa alternativa a considerar quando há um número relativamente elevado de número de cargas armazenadas em relação ao número de unidades mantidas em armazém (SKUs) ou unidades em armazém individualmente identificáveis. Quando isto acontece, não é necessário acesso total a todas as cargas. Cargas semelhantes podem ser armazenadas uma atrás da outra mas movimentadas juntas num ciclo da grua. Este conceito aumenta a densidade do armazenagem da carga no sistema de 10 a 20% comparado com a armazenagem de profundidade simples.


B. Considerações especiais de projeto

A actividade em particular pode também requerer considerações de projeto no sistema que podem afectar o planeamento e orçamento global. Assegure-se são considerados fatores tais como:

O projecto do edifício novo é do tipo suportado pelas estantes?

É preciso ter capacidade de picking de encomendas?

Os produtos necessitam de armazenamento a baixas temperaturas?

É necessária proteção especial contra incêndios?

(Alesly, 2006u)


9. Custo de um sistema de armazenagem automática

Segue-se a estimativa do orçamento para o equipamento, de acordo com procedimentos de custeio correntes. Estes preços incluem materiais, engenharia e mão de obra. Em todos os casos, é dado um intervalo do custo para levar em consideração variáveis, tais como, cargas leves vs. pesadas, a complexibilidade dos equipamentos e controlo necessários, e diferenças locais nos custos laborais. Sugere-se que se estime o orçamento para o sistema planeado usando os valores mais altos e mais baixos do intervalo nos cálculos que se seguem. Note-se que estes dados de custos incluem o controlo por computador para automação total o que, normalmente, não representa mais de 10% do custo total do sistema. Os muitos benefícios da automação, incluindo a operação do sistema à capacidade máxima com um mínimo de mão de obra, mais um mínimo de danificação dos produtos, compensam largamente os custos.

Lembre-se, o objectivo principal de um computador, usado como controlador de um sistema, é assegurar que a capacidade operacional do equipamento, gruas e transportadores é atingida. O arquivo de informação é uma capacidade adicional de baixo custo.

Planear um sistema manual pensando em convertê-lo mais tarde num sistema automático é um erro. Raramente é viável converter, satisfatoriamente, um sistema manual, em funcionamento, num automático. O longo tempo de paragem necessário para instalar todas as componentes do sistema para se fazer conversão custa muito mais do que o investimento inicial na automação. Se se tem que economizar inicialmente, considere-se diminuir o comprimento do sistema (número de locais de armazenagem necessários) porque é relativamente fácil aumentar o comprimento do sistema sem interromper as operações do sistema (Alesly, 2006t).


Armazenagem Dedicada Baseada em Classes
Considere-se a afectação de classes de artigos a locais de armazenagem num AS/RS usado para armazenar paletes inteiras dos produtos. Uma vista de um dos lados de um corredor do armazem é dado é mostrada na Figura 8.19. A estante tem 10 níveis de armazenagem verticalmente e 40 colunas de armazenagem horizontalmente. O local de entrada e saída (I/O) do sitema está a 2,3 m (7,5 pés) do fim para do coreedor e elevado de 6 m (20 pés). Os locais de armazenagem têm 1,5 m × 1,5 m (5 pés × 5 pés) de tamanho. A máquina de S/R desloca-se horizontalmente à velocidade de 76,2 m/min (250 pés/min); desloca-se verticalmente à velocidade de 15,24 m/min (50 pés/min). Além disso, a S/R desloca-se vertical e horizontalmente em simultâneo; portanto o tempo necessário para a deslocação entre dois postos é o máximo do tempo para a deslocação horizontal e do tempo para a deslocação vertical. A S/R desloca-se para o ponto médio do nível de suporte da carga de cada local de armazenagem. Todas as deslocações são entre um local de armazenagem e o ponto de entrada e saída (I/O).


Figura 8.19. Vista de um dos lados de um corredor do armazenagem
(carregar com o cursor na figura para ver em tamanho grande)

Para ilustrar o cálculo do tempo de deslocação, considere-se o movimento da S/R do I/O para o local de armazenagem no nível superior da segunda coluna de armazenagem. A distância horizontal a ser percorrida para o ponto médio do nível da base é 4,57 m (15 pés); a distância vertical é 7,62 m (25 pés). O tempo necessário para a deslocação horizontal é 4,57 / 76,2 (15 / 250) ou 0,06 minutos; o tempo necessário para deslocação vertical é 7,62 / 15,24 (25 / 50) ou 0,5 minutos. Então o tempo de deslocação entre o I/O e o local de armazenagem é o máximo de 0,06 e 0,5, ou 0,5 minutos.

O corredor de armazenamento tem 800 locais de armazenagem, uma vez que o armazenamento ocorre em ambos os lados de corredor. Estão para ser armazenadas quatro classes de produtos. Uma classe necessita de 80 locais de armazenagem e tem uma movimentação de 27 operações por hora, em que uma operação é definida como sendo de armazenar ou retirar uma carga. A segunda classe necessita de 172 locais de armazenagem e tem uma necessidade de movimentações de 15 operações por hora. A terceira classe necessita de 248 locais de armazenagem e tem uma movimentação de 6 operações por hora. A quarta classe necessita de 300 locais de armazenagem e tem uma movimentação de 2 operações por hora. Cada operação necessita de 0,25 minutos para levantar ou depositar (P/D) uma carga.

As razões das movimentação em relação aos espaços de armazenagem dos produtos indicam que as classes devem ser numeradas na mesma sequência em que foram identificadas acima. A configuração resultante é dada na Figura 8.20. A mesma configuração aplica-se a ambos os lados de corredor.

Figura 8.20. Atribuição de classes a locais de armazenagem
(carregar com o cursor na figura para ver em tamanho grande)

Para determinar a utilização da S/R, note-se que é realizado um total de 50 operações por hora e que cada operação necessita que uma carga seja levantada ou depositada. Portanto 25 minutos são gastos por hora na realização das necessidades de P/D. Isto deixa 35 minutos por hora para as deslocações para e dos locais de armazenagem.

Supõe-se que cada lugar atribuído a uma classe tem igual probabilidade de ser seleccionado para armazenagem ou retirada. O tempo da viagem de ida e volta para os produtos da classe 1 é de 0,3040 minutos; para os produtos da classe 2, 0,5977 minutos; para o produto de classe 3, 0,9016 minutos; e para os produto da classe 4, 1,36 minutos. Portanto as deslocações por hora totalizam 27 (0,3040) + 15 (0,5977) + 6 (0,9016) + 2 (1,360) ou 25,303 minutos. Portanto a utilização horária é (25 + 25,303) / 60 ou 83,8% (Francis et al., 1992 e Alesly, 2006v).


Configuração de Área de Armazenagem Contínua
Num AS/RS, as movimentações ocorrem simultaneamente na horizontal e vertical. Suponha-se que o ponto de I/O se localiza na origem e a zona de armazenamento vai ser construída no primeiro quadrante. A movimentação horizontal ocorre à velocidade de 121,92 m/min (400 pés/min) e a movimentação vertical ocorre à velocidade de 24,38 m/mim (80 pés/min).

O tempo necessário para a movimentação do ponto de I/O localizado na origem (0,0) para uma localização de coordenadas (x, y) é dado por

T_{x, y} = max {x / 400, y / 80}

Dado que a velocidade horizontal é cinco vezes maior que a velocidade vertical, a curva de nível das movimentações do I/O será um rectângulo com um comprimrnto igual a 5 vezes a altura. Se H for a altura, a área (A) envolvida por uma curva de nível será A = 5 H². Se é necessária uma área A = 1 672 m² (18 000 pés²), resolvendo para o valor de H obtém-se um valor de 18,29 m (60 pés). Então, as forma e dimensões da zona de armazenagem deve ser rectangular com uma altura de 18,29 m (60 pés) e um comprimento de 91,44 m (300 pés) de modo a minimizar o tempo médio de movimentação do I/O para um local de armazenagem aleatório (Alesly, 2006w).


Tempo Médio de S/R
Para ilustrar o cálculo do tempo médio de movimentação para outras distâncias sem serem rectilineares, considere-se um corredor de armazenamento de um AS/RS com o I/O localizado no canto inferior esquerdo da zona de armazenagem. Designe-se por t_h o tempo necessário para a movimentação horizontal do I/O para o ponto mais distante de armazenagem e t_v o tempo necessário para a movimentação vertical do I/O para o ponto mais distante do armazém, com t_v < t_h.

Uma curva de nível do tempo de movimentação tem forma rectangular, como se mostra na Figura 8.21. Continue-se a designar por A a área a ser envolvida pela curva de nível e faça-se k igual ao valor da curva de nível. Para k < t_v, a curva de nível é quadrada em unidades de tempo e de dimensões k × k; para k > t_v, a curva de nível é rectangular, de altura t_v e comprimento k. Portanto, a determinação do tempo esperado de movimentação é realizada em dois passos.

Figura 8.21. Curvas de nível para um sistema de armazenamento automático (AS/RS)
(carregar com o cursor na figura para ver em tamanho grande)

Considere-se primeiro a curva de nível quadrada em unidades de tempo. A área envolvida pela curva de nível é k². Portanto, A = k² = q (k), k = A^1/2 = r (A) e 0 < k < t_v.

Para o segundo conjunto de curvas de nível, o valor da curva de nível é k; a área envolvida pela curva de nível é k t_v. Então, A = k t_v = q (k), k = A / t_v e t_v < k < t_h, uma vez que A = t_v t_h.

O tempo esperado de deslocação é dado por:
(carregar com o cursor na equação para ver em tamanho grande)
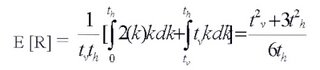
Fazendo t_v = b t_h, onde 0 < b <>E[R] = t_h(b² + 3) / 6
Relembre-se que E[R] é baseado em movimentações de um só sentido. Para movimentações de ida e volta o valor obtido deve ser duplicado (Alesly, 2006x).

Referências

CHOPRA, Sunil; MEINDL, Peter - Supply Chain Management: Strategy, Planning, and Operation, 2.ª ed. Upper Saddle River, NJ, Pearson International Editions, 2004.

FRANCIS, Richard L. et al. - Facility Layout and Location: An Analytical Approach, 2.ª ed., Englewood Cliffs, NJ, Prentice Hall, 1992.

GLICKMAN, Rick; SCHEMMEL, Jim - MTAC Summary. Washington, United States Postal Service, 1997. Consultado a 20 de Maio de 2006.

GUE, Kevin R. - Crossdocking: Just-In-Time for Distribution. Monterey, CA, Naval Postgraduate School, 2001. Consultado a 10 de Março de 2006.

HARNISCHFEGER P&H. Milwaukee, WI, (s.d.) - 9 Simple Steps to Determine the Layout, Design and Estimated Cost of an Automated Storage / Retrieval System.

KIM, David S. - The Ten Principles of Material Handling. Corvallis, Oregon State University, 2005. Consultado a 20 de Maio de 2006.

MUTHER, Richard – Planejamento do Layout: Sistema SLP. São Paulo, Edgar Blücher, 1978.

TIGERLOG. São Paulo - Movimentação e armazenagem. Consultado a 21 de Março de 2006.

TOMPKINS, James A.; WHITE, John A. - Facilities Planning, Nova Iorque, John Wiley & Sons, 1984.

TOMPKINS, James A. et al. - Facilities Planning, 2.ª ed., Nova Iorque, John Wiley & Sons, 1996.

WIKIPÉDIA - Stock Keeping Unit. Consultado a 23 de Maio de 2006.

ZOLLINGER, H. A. - Planning, Evaluating, and Estimating Storage Systems. «Institute of Material Mangement Education First Annual Winter Seminar Series», Orlando, FL, Fev. 1982.


Ligações

Asociación Española de Codificiación Comercial (AECOC). Barcelona - RAL sobre los procesos de Cross Docking. Consultado a 23 de Abril de 2006.