V. Planeamento e Projecto de Hipermercados (Continuação)
Localização numa Rede Cíclica
1. A localização potencial da instalação a ser localizada - ou num nó ou em qualquer ponto da rede.
2. A localização das procuras - ou num nó ou em qualquer ponto da rede.
3. Função objectivo - ou minimizar o custo total a todos os pontos de procura ou minimizar o custo máximo a qualquer ponto de procura.
Este esquema da classificação é resumido na Figura 5.20.
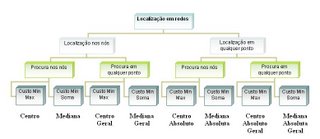 Figura 5.20. Classificação dos problemas de localização de um
Figura 5.20. Classificação dos problemas de localização de umcentro de distribuição / hipermercado numa rede
(carregar com o cursor na figura para ver em tamanho grande)
Cada combinação das características do problema tem um nome diferente como se mostra na figura. Estes são definidos abaixo:
1. Um centro de uma rede é qualquer nó cujo nó mais distante está tão perto quanto possível. Neste caso, tanto a instalação como as procuras ocorrem somente em vértices.
2. Um centro geral de uma rede é qualquer nó cujo ponto mais distante na rede está tão perto quanto possível. Note-se que enquanto a instalação é localizada num vértice, os pontos de procura encontram-se ao longo dos arcos da rede assim como nos nós.
3. Um centro absoluto de uma rede é qualquer ponto cujo nó mais distante está tão perto quanto possível. Neste caso, a instalação é localizada em qualquer ponto da rede, mas as procuras ocorrem somente nos nós.
4. Um centro absoluto geral de uma rede é qualquer ponto cujo ponto mais distante estiver tão perto quanto possível. Aqui, tanto a instalação como as procuras localizam-se em qualquer ponto da rede.
Por analogia a cada um destes quatro tipos de problemas de localização numa rede, pode-se definir a mediana, mediana geral, mediana absoluta, mediana absoluta geral, mudando simplesmente a função objectivo de minimizar a distância máxima da instalação a uma procura, pela de minimizar a soma das distâncias da instalação a todos os pontos de procura (Carla, 2006m).
A mediana é qualquer nó x de uma rede com a menor distância total possível de x a todos os outros nós. Assim, uma mediana é é qualquer nó x tal que
SVV (x) = min {SVV (i)}
onde
SVV (i) = ∑ d (i, j)
A soma dos valores da linha i da matriz das distâncias mais curtas entre todos os pares de nós, D, é igual à soma das distâncias do nó i a todos os outros nós, isto é, SVV (i). Então, uma mediana corresponde a qualquer linha de D com a menor soma.
A matriz das distâncias mais curtas entre todos os pares de nós, D, da rede da Figura 5.21 é
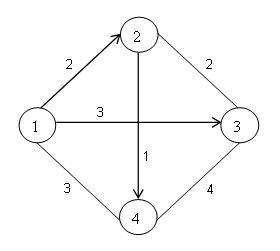
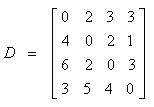
Portanto,
SVV (1) = 0 + 2 + 3 + 3 = 8
SVV (2) = 4 + 0 + 2 + 1 = 7
SVV (3) = 6 + 2 + 0 + 3 = 11
SVV (4) = 3 + 5 + 4 + 0 = 12
Então, min {SVV (i)} = min {8, 7, 11, 12} = 7 = SVV (2), e o nó 2 é a mediana desta rede. A distância total do nó 2 a todos os outros nós é 7 unidades (Carla, 2006a).
Considere-se a distância mais curta do nó j a cada ponto do arco (r, s). Para algum ponto do arco (r, s), esta distância tem o seu valor máximo. Esta distância máxima do nó j a qualquer ponto no arco (r, s) é denotada por d' (j, (r, s)) e chama-se distância nó-arco.
Se o arco (r, s) não tem direcção, há duas meaneiras de ir do nó j ao ponto f em (r, s): via nó r ou via nó s. Naturalmente, selecciona-se a mais curta das duas rotas. Se estas duas rotas têm distâncias desiguais, então alguns pontos na vizinhança do ponto f do arco(r, s) estão ainda mais afastados do nó j. Por exemplo, na Figura 5.22, o ponto 0,25 do arco (3, 4) está a 1,25 unidades ou 2,75 unidades do nó 2, conforme se vá via nó 3 ou via nó 4. Se o f é aumentado de 0,25 para 0,26, a distância mais curta do nó 2 ao ponto 0,26 do arco (3, 4) é o min {1,26; 2,74} = 1,26. Estas duas distâncias são iguais no ponto mais distante. Observe-se que essas duas distâncias somam sempre
d (j, r) + f a (r, s) + d (r, s) + (1 - f) a (r, s) = d (j, r) + d (j, s) + a (r, s)
Então, segue-se que
d' (j, (r, s)) = [d (j, r) + d (j, s) + a (r, s)] / 2 (2a)
Se, por outro lado, o arco (r, s) é direccionado, então um ponto no arco (r, s) só pode ser alcançado via nó r. Consequentemente, os pontos mais distantes de (r, s) de qualquer nó são os pontos mais próximos do nó s, isto é, os pontos f para os quais f se aproxima de 1. Neste caso
d' (j, (r, s)) = d (j, r) + a (r, s) (2b)
Numere-se os arcos numa rede G de 1 a m. Denote-se por D' a matriz n × m cujo elemento j, k é a distância do nó-arco do nó j ao arco k. Observe-se que a matriz das distância do nó–arco D' pode ser calculada da matriz das distâncias entre todos os pares de nós D e o comprimento dos arcos usando as equações (2a) e (2b) (Carla, 2006k).
Uma mediana geral é qualquer nó x com a menor distância total a cada arco, onde a distância de um nó a um arco é a distância máxima do nó aos pontos do arco. Portanto, uma mediana geral é qualquer nó x tal que
SVA (x) = min {SVA (i)}
onde
SVA (i) = ∑ d' (i, (r, s)
A soma dos valores na linha i da matriz das distâncias mais curtas entre todos os pares (nós, arcos), D´, é igual à soma das distâncias do nó i a todos os arcos, isto é, SVA (i). Portanto, uma mediana geral corresponde a qualquer linha de D' com a menor soma.
Ordenando os arcos da Figura 5.21 como se segue,
1. (1, 2)
2. (1, 3)
3. (1, 4)
4. (2, 4)
5. (2, 3)
6. (3, 4)
a matriz das distâncias mais curtas entre todos os pares (nós, arcos), D', da rede da Figura 5.21 é

Portanto,
SVA (1) = 2 + 3 + 3 + 3 + 3,5 + 5 = 19,5
SVA (2) = 6 + 7 + 4 + 1 + 2 + 3,5 = 23,5
SVA (3) = 8 + 9 + 6 + 3 + 2 + 3,5 = 31,5
SVA (4) = 5 + 6 + 3 + 6 + 5,5 + 4 = 29,5
Então, min {SVA (i)} = min {19,5; 23,5; 31,5; 29,5} = 19,5 = SVA (1). Assim, o nó 1 é a mediana geral desta rede. A distância total do nó 1 a todos os arcos é 19,5 unidades (Carla, 2006b).
Uma mediana absoluta é qualquer ponto com a menor distância total possível a todos os nós. A distância de um ponto a um nó é a distância mais curta do ponto ao nó. Então, a mediana absoluta geral é qualquer ponto f – (r, s) tal que
SPV (f – (r, s)) = min SPV (f – (t, u)), com f – (t, u) ∈ P, o conjunto de todos os pontos da rede
onde
SPV (f – (t, u)) = ∑ d (f – (t, u), j)
Considerando que SPV (f – (r, s)) é uma função côncava de f,
então é minimizada quando f = 0 ou f = 1.
Consequentemente, nenhum ponto interior do arco (r, s) é um candidato melhor para mediana absoluta do que um dos seus nós terminais.
Então só é necessário considerar os nós na procura de uma mediana absoluta, qualquer mediana é também uma mediana absoluta e não são necessárias novas técnicas de resolução (Carla, 2006h).
Represente-se por d' (f – (r, s), (t, u)) a distância máxima do ponto f do arco (r, s) aos pontos do arco (t, u). Esta é a chamada distância ponto-arco.
Se o arco (r, s) não tem direcção e se (r, s) ≠ (t, u), então a rota do ponto f de (r, s) ao ponto mais distante de (t, u) deve ser ou via nó r ou via nó s. Então, segue-se que
d' (f – (r, s), (t, u)) = min {f a (r, s) + d' (r, (t, u)), (1 – f) a (r, s) + d' (s, (t, u))} (3a)
Se o arco (r, s) é direccionado e (r, s) ≠ (t, u), o primeiro termo da minimização acima pode ser eliminado e
d' (f - (r, s), (t, u)) = (1 - f) a (r, s) + (d´ (s, (t, u)) (3b)
Se (r, s) = (t, u) e se o arco (r, s) é direccionado, os pontos mais distantes, do arco (r, s), do ponto f de (r, s) são os pontos g tais que g se aproxima de f de valores menores que f. Assim, neste caso,
d' (f - (r, s), (r, s) = (1 - f) a (r, s) + d (s, r) (3c)
Se (r, s) = (t, u) e se o arco (r, s) não tem direcção, a distância máxima do ponto f de (r, s) para qualquer ponto g de (r, s) (onde g < f) não pode exceder
A = min {f a (r, s), [a (r, s) + d (s, r)] / 2}
O primeiro termo desta minimização leva em conta as rotas do ponto f ao ponto g limitado ao arco (r, s). O segundo termo da minimização leva em conta as rotas do ponto f de (r, s) ao ponto g de (r, s) que passam pelo nó s.
Similarmente, a distância máxima do ponto f de (r, s) a qualquer ponto g de (r, s) (onde g > f) não pode exceder
B = min {(1 - f) a (r, s), [a (r, s) + d (s, r)] / 2}
O primeiro termo da minimização precedente leva em conta as rotas do ponto f ao ponto g limitado ao arco (r, s). O segundo termo da minimização precedente leva em conta as rotas do ponto f de (r, s) ao ponto g em (r, s) que passam pelo vértice r.
Consequentemente, se o arco (r, s) não tem direcção,
d' (f - (r, s), (r, s)) = max {A, B}
ou, equivalentemente,
d' (f - (r, s), (r, s)) = max {min {f a (r, s), [a (r, s) + d (s, r)] / 2}}, min {(1 - f) a (r, s), [a (r, s) + d (r, s)] / 2}} (3d)
Quando d' (f - (r, s), (t, u)) é traçado em função de f para todos os (r, s) ≠ (t, u), a curva toma a mesma forma que nas distâncias ponto-nó mostradas na Figura 5.24, dado que a equação (3a) tem a mesma forma que a equação (1a) e a equação (3b) tem a mesma forma que a equação (1b). Só as constantes são diferentes; as formas equacionais são as mesmas.
Por outro lado, quando d' (f - (r, s), (r, s)) é traçado em função de f para qualquer arco sem direcção (r, s), a curva toma a forma apresentada na Figura 5.23. Isto decorre da equação (3d) (Carla, 2006l).

(carregar com o cursor na figura para ver em tamanho grande)
Uma mediana absoluta geral é qualquer ponto com a propriedade de que a distância total do ponto a todos os arcos é a menor possível. A distância de um ponto a um arco é a distância máxima do ponto a todos os pontos do arco. Então, a mediana absoluta geral é um ponto qualquer f – (r, s) tal que
SPA (f – (r, s)) = min SPA (f – (t, u)), com f – (t, u) ∈ P, o conjunto de todos os pontos da rede
onde
SPA (f – (t, u)) = ∑ d' (f – (t, u), (v, w))
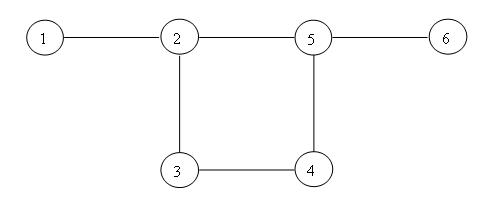
Para encontrar a mediana absoluta geral da rede da Figura 22, usa-se o o algoritmo de Floyd ou o algoritmo de Dantzig, para determinar a matriz das distâncias mais curtas entre todos os pares de nós, D, da rede.

Seguidamente, ordenam-se os arcos como se segue:
1. (1, 2)
2. (2, 3)
3. (3, 4)
4. (4, 5)
5. (5, 6)
6. (2, 5)
Da equação (2a),
d' (j, (r, s) = 0,5 [d (j, r) + d (j, s) + a (r, s)]
pode-se calcular a matriz das distâncias nó - arco, D', obtendo-se
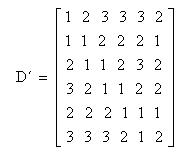
Portanto,
SVA (1) = 1 + 2 + 3 + 3 + 3 + 2 = 14
SVA (2) = 1 + 1 + 2 + 2 + 2 + 1 = 9
SVA (3) = 2 + 1 + 1 + 2 + 3 + 2 = 11
SVA (4) = 3 + 2 + 1 + 1 + 2 + 2 = 11
SVA (5) = 2 + 2 + 2 + 1 + 1 + 1 = 9
SVA (6) = 3 + 3 + 3 + 2 + 1 + 2 = 14
Consequentemente, os nós 2 e 5 são os melhores nós candidatos a mediana absoluta geral uma vez que cada um destes nós tem uma distância total a todos os arcos igual a 9 unidades.
Em seguida, tenta-se eliminar o interior de alguns arcos (Carla, 2006c).
Um centro é qualquer nó x com o menor valor possível de MVV (x); isto é, um centro é qualquer nó x tal que o nó mais distante de x está tão perto quanto possível,
MVV (x) = min {MVV (i)}
onde
MVV (i) = max { d (i, j)}
O algoritmo de Floyd ou o algoritmo de Dantzig podem ser usados para calcular a matriz das distâncias nó - nó, D, cujo elemento i, j é d (i, j), a distância mais curta do nó i ao nó j. A distância máxima MVV (i) do nó i a qualquer nó é o maior elemento da linha i da matriz D. Um centro é qualquer nó x com o menor valor possível de MVV (x); isto é, um centro é qualquer nó cuja a linha na matriz D tem o menor valor máximo.
Para encontrar o centro da rede da Figura 5.21, a matriz das distâncias mais curtas entre todos os pares de nós, D, usando o algoritmo de Floyd ou o de Dantzig, é
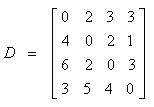
Então,
MVV (1) = max {0, 2, 3, 3} = 3
MVV (2) = max {4, 0, 2, 1} = 4
MVV (3) = max {6, 2, 0, 3} = 6
MVV (4) = max {3, 5, 4, 0} = 5
Então, min MVV (i) = min {3, 4, 6, 5} = 3 = MVV (1). Consequentemente, o nó 1 é um centro desta rede. O nó mais distante do nó 1 está a 3 unidades de distância. Nenhum outro nó está a menos de 3 unidades (Carla, 2006d).
Um centro geral é qualquer nó x com o menor valor possível de MVA (x), isto é, um nó qualquer tal que o ponto mais distante do nó x está tão perto quanto possível,
MVA (x) = min {MVA (i)}
onde
MVA (i) = max d' (i, (r, s)
Um centro geral pode ser encontrado procurando a linha de D' com o elemento de menor valor máximo. Esta fila corresponde a um nó que é um centro geral. Isto resulta de MVA (i) ser o maior elemento da linha i da matriz das distâncias nó - arco D'.
Para determinar o centro geral da rede da Figura 5.21, os arcos da rede são numerados de 1 a 6, como se segue,
1. (1, 2)
2. (1, 3)
3. (1, 4)
4. (2, 4)
5. (2, 3)
6. (3, 4)
Usando a matriz das distâncias mais curtas entre todos os pares de nós, D (Localização central) e os comprimentos dos arcos dados na Figura 5.21, pode usar-se as equações (2) para calcular a matriz D'.
A equação (2a) para arcos (r, s) sem direcção ou com dois sentidos,
d' (j, (r, s) = 0,5 [d (j, r) + d (j, s) + a (r, s)]
E a equação (2b) para arcos (r, s) com direcção ou com um sentido,
d' (j, (r, s) = d (j, r) + a (r, s)
Por exemplo, da equação (2a),
d' (1, (3, 4)) = 0,5 [d (1, 3) + d (1, 4) + a (3, 4)] = 0,5 (3 + 3 + 4) = 5
Da equação (2b),
d' (1, (2, 4)) = d (1, 2) + a (2, 4) = 2 + 1 = 3
Então,

Portanto,
MVA (1) = max {2, 3, 3, 3, 3,5; 5} = 5
MVA (2) = max {6, 7, 4, 1, 2, 3,5} = 7
MVA (3) = max {8, 9, 6, 3, 2, 3,5} = 9
MVA (4) = max {5, 6, 3, 6, 5,5; 4} = 6
Então, min MVA (i)= min {5, 7. 9. 6} = 5 = MVA (1). Assim, o nó 1 é um centro geral da rede. O ponto mais afastado do nó 1 dista 5 unidades do nó 1 e fica no arco (3, 4) (Carla, 2006e).
Represente-se por d (f - (r, s), j) o comprimento do caminho mais curto do ponto f do arco (r, s) ao nó j. Esta é a chamada distância ponto-nó. Se o arco (r, s) não tem direcção, i.e., permite movimentações em ambas as direcções, esta distância deve ser a menor das duas distâncias seguintes:
a) a distância do ponto f ao nó r mais a distância do nó r ao nó j;
b) a distância do ponto f ao nó s mais a distância do nó s ao nó j.
Então,
d (f - (r, s), j) = min {f a (r, s) + d (r, j), (1 – f) a (r, s) + d (s, j)} (1a)
Se (r, s) é um arco direccionado, i.e., só são permitidas movimentações de r para s, o primeiro termo da minimização acima é eliminado e
d (f - (r, s), j) = (1 – f) a (r, s) + d (s, j) (1b)
Observe-se que só os comprimentos dos arcos e a matriz de D são necessários para calcular todas as distâncias ponto-nó.
Quando traçada em função de f, a distância ponto-nó para um dado arco (r, s) e um dado nó j toma uma das três formas mostradas na Figura 5.24. Note-se que o declive desta curva linear quebrada é ou + a (r, s) ou – a (r, s) e declive faz na máximo uma mudança de + a (r, s) para – a (r, s) (Carla, 2006j).

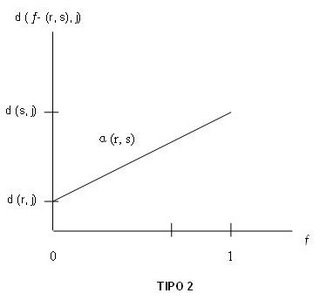
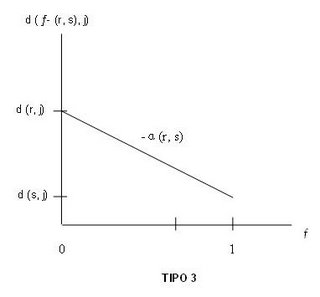 Figura 5.24. Gráficos de distâncias ponto-nó.
Figura 5.24. Gráficos de distâncias ponto-nó.Um centro absoluto é um ponto qualquer cujo nó mais distante está tão perto quanto possível. Para encontrar um centro absoluto, tem que se encontrar o ponto f – (r, s) tal que
MPV (f – (r, s)) = min MPV (f – (t, u)), com f – (t, u) ∈ P, o conjunto de todos os pontos da rede
onde
MPV (f – (t, u)) = max {d (f – (t, u), j)}
Para encontrar um centro absoluto para a rede da Figura 5.21, sabe-se que todos os centros absolutos (pode haver empates e, consequentemente, mais de que um centro absoluto) devem ser nós ou pontos interiores de arcos sem direcção ou com dois sentidos. Nenhum ponto interior de um arco com direcção ou sentido único pode ser um centro absoluto. Uma vez que todas as movimentações num arco com direcção é numa direcção, segue-se que o nó terminal de um arco com direcção está mais perto de cada nó na rede do que qualquer ponto interior do arco com sentido único.
O melhor nó candidato a centro absoluto seria o nó seleccionado como centro. No cálculo do centro desta rede, resultou que o nó 1 era o centro e todos os nós estavam a 3 ou menos unidades do nó 1. Então, o nó 1 é o melhor nó candidato com um alcance de 3 unidades.
Resta examinar o interior dos três arcos sem direcção (1, 4), (2, 3) e (3, 4).
Primeiro, examine-se o arco (3, 4). Da equação (1a),
d (f – (r, s), j) = min {f a (r, s) + d (r, j), (1 – f) a (r, s) + d (s, j)}
tem-se,
d (f – (3, 4), 1) =
= min {f a (3, 4) + d (3, 1), (1 – f) a (3, 4) + d (4, 1)} =
= min {4 f + 6, 4 (1 – f) + 3} =
= 4 f + 6, para f ≤ 0,125
= 7 – 4 f, para f ≥ 0,125
d (f – (3, 4), 2) =
= min {f a (3, 4) + d (3, 2), (1 – f) a (3, 4) + d (4, 2)} =
= min {4 f + 2, 4 (1 – f) + 5} =
= 4 f + 2, para f ≤ 0,875
= 9 – 4 f, para f ≥ 0,875
d (f – (3, 4), 3) = min {f a (3, 4) + d (3, 3), (1 – f) a (3, 4) + d (4, 3)} =
= min {4 f , 4 (1 – f) + 4} =
= 4 f, para qualquer f, 0 ≤ f ≤ 1
d (f – (3, 4), 4) = min {f a (3, 4) + d (3, 4), (1 – f) a (3, 4) + d (4, 4)} =
= min {4 f + 3, 4 (1 – f) + 0} =
= 4 f + 3, para f ≤ 0,125
= 4 – 4 f, para f ≥ 0,125
(Carla, 2006g).
Estas distâncias ponto - nó são apresentadas na Figura 5.25. O valor mais baixo da secção mais elevada destas curvas ocorre quando,
d (f – (3, 4), 1) = d (f – (3, 4), 2).
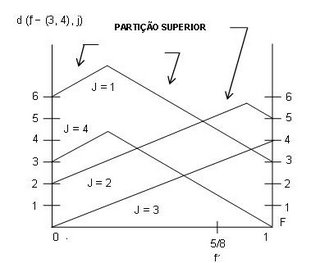
(carregar com o cursor na figura para ver em tamanho grande)
Então,
7 - 4 f* = 4 f* + 2
f* = 0,625
d (0,625 – (3, 4), 1) = d (0,625 – (3, 4), 2) = 4,5
Consequentemente, o ponto 0,625 é o melhor candidato para centro absoluto no arco (3, 4) e nenhum nó está a mais de 4,5 unidades do ponto 0,625 do arco (3, 4).
A Figura 5.26 mostra o mesmo resultado para o arco (1, 4). Note-se que o melhor candidato para centro absoluto no arco (1, 4) é o ponto 0 que é o nó 1. Conforme já visto, sabe-se que todos os nós estão a 3 unidades de distância ou menos do nó 1.

(carregar com o cursor na figura para ver em tamanho grande)
A Figura 5.27 mostra o mesmo resultado para o arco (2, 3). Note-se que o melhor candidato para centro absoluto no arco (2, 3) é o ponto 0 que é o nó 2. Conforme já visto, sabe-se que todos os nós estão a 4 unidades de distância ou menos do nó 2.

(carregar com o cursor na figura para ver em tamanho grande)
Consequentemente, o ponto interior melhor candidato é o ponto 0,625 no arco (3, 4) com uma distância máxima de 4,5 unidades. O nó melhor candidato é o nó 1 com uma distância máxima de 3 unidades. Portanto, o nó 1 é o centro absoluto desta rede (Carla, 2006f).
Um centro absoluto geral é qualquer ponto x tal que o ponto mais afastado do ponto x está tão perto quanto possível. Para encontrar um centro absoluto geral, tem que se encontrar um ponto f – (r, s) tal que
MPA (f – (r, s)) = min {MPA (f – (t, u))}, com f – (t, u) ∈ P, o conjunto de todos os pontos da rede
onde
MPA (f – (t, u)) = max {d' (f – (t, u), (v, w))}
Para encontrar um centro absoluto geral, sabe-se que todos os centros absolutos gerais (pode haver empates e, consequentemente, mais de que um centro absoluto geral) devem ser nós ou pontos interiores de arcos sem direcção ou com dois sentidos. Nenhum ponto interior de um arco com direcção ou sentido único pode ser um centro absoluto geral. Uma vez que todas as movimentações num arco com direcção é numa direcção, segue-se que o nó terminal de um arco com direcção está mais perto de cada arco na rede do que qualquer ponto interior do arco com sentido único. Consequentemente, para encontrar um centro absoluto geral só é preciso considerar nós e pontos interiores de arcos sem direcção ou com dois sentidos.
Observe-se que o problema de encontrar um centro absoluto geral é idêntico ao problema de encontrar um centro abslouto, excepto quando agora tem que se considerar as distâncias ponto - arco, em vez das distâncias ponto - nó. Todas as funções distância ponto - arco têm a mesma forma que as funções distância ponto - nó, excepto a distância ponto - arco d' (f – (r, s), (r, s)).
Na maioria dos problemas reais, o ponto mais distante do ponto f no arco (r, s) não se encontra no arco (r, s). Neste caso, pode-se simplesmente omitir de se continuar a considerar a função distância do ponto - arco d' (f - (r, s), (r, s)). O problema de encontrar um centro absoluto geral pode agora ser resolvido pela técnica usadas para encontrar um centro absoluto. A única diferença é que as funções distância ponto - arco têm que substituir a função distância ponto - nó. Como há mais arcos do que nós, é necessário fazer mais gráficos para se encontrar o centro absoluto geral.
Se, no entanto, houver uma possibilidade do ponto mais distante do ponto f no arco (r, s) também se encontra no arco (r, s), então o gráfico da função distância ponto-arco d' (f - (r, s), (r, s)), tem que ser incluído nos cálculos para o melhor candidato no arco (r, s). A equação (3d) pode ser usada para construir esse gráfico. Felizmente, este gráfico também é uma linha quebrada com um máximo de quatro secções.
Em resumo, a técnica para se encontrar um centro absoluto geral é a mesma que a técnica para se encontrar um centro absoluto excepto que as distâncias do ponto - nó são substituídas pelas distâncias do ponto - arco (Carla, 2006i).


0 Comments:
Post a Comment
<< Home