V. Planeamento e Projecto de Hipermercados (Continuação)
Solução Gráfica
Dados dois pontos A e B num sistema de eixos cartesiano x e y, a distância rectilinear ou rectangular, entre A e B, obtém-se somando a distância segundo a direcção x com a distância segundo a direcção y. Todos os pontos situados num quadrado com as diagonais paralelas aos eixos, centro em A e que passa por B, estão à mesma distância de A que o ponto B.
Considere-se, então, o problema de determinar a localização de um armazém central para abastecer uma rede de 6 hipermercados, todos com aproximadamente a mesma dimensão e volume de vendas de modo a minimizar a distância máxima do armazém aos hipermercados. As coordenadas dos hipermercados já existentes (Figura 5.1) são: (9, 13), (9, 18), (10, 7), (14, 15), (15, 15) e (16, 6). Desenhe-se o menor rectângulo possível que inclua todas as localizações dos hipermercados (os pontos podem ficar sobre uma aresta ou dentro do rectângulo) e cujas arestas façam um ângulo de 45º com um dos eixos. Extenda-se as arestas de menor comprimento (se necessário), até formar um quadrado. Uma dessas extensões possíveis é representada, na Figura 5.1, pelas linhas a tracejado e a outra pelas linhas a ponteado.

(carregar com o cursor na figura para ver em tamanho grande)
Fonte: Francis et al., 1992
Unindo os vértices 1 e 2 e os vértices 3 e 4, na intersecção dessas duas linhas obtém-se o centro do quadrado e uma localização óptima, com as coordenadas (13,5; 13). Unindo os vértices 5 e 6 e os vértices 7 e 8, obtém-se, na intersecção das diagonais deste quadrado, o ponto (10,5; 10), outra localização óptima para o armazém. Cada quadrado tem uma semi diagonal de 9,5, que é o menor valor da distância máxima entre um hipermerdo e o armazém central. Qualquer quadrado com uma semi diagonal de 9,5, com o centro sobre o segmento de recta que une os pontos (10,5, 10) e (13,5; 13) também cobre todos os pontos e, portanto, também é óptimo. Pode-se, então, concluir que qualquer local sobre o seguemento de recta que une os pontos (10,5, 10) e (13,5; 13) é uma localização óptima para o armazém central e o menor valor da distâcia de qualquer hipermacado ao armazém é 9,5 (Marco, 2006f).
Solução Numérica
Para resolver o problema, aplicando um método analítico, (ai; bi) correspondem às coordenadas dos hipermercados. Como as distâncias apropriadas são rectilíneares e todas as deslocações são feitas ao mesmo custo por unidade de distância ou têm a mesma importância, o problema é minimizar a função:
f(x, y) = máximo {(│x - ai│+│y - bi│): i = 1, …,m}
Calculando os números:
c1 = mínimo {ai + bi: i = 1, …, m}
c2 = máximo {ai + bi: i = 1, …, m}
c3 = mínimo {-ai + bi: i = 1, …, m}
c4 = máximo {-ai + bi: i = 1, …, m}
c5 = máximo {c2 - c1, c4 - c3}.
O valor mínimo da função objectivo é c5 / 2 e as localizações minimax são os locais no segmento de recta L que une os seguintes dois pontos:
(x1, y1) = ½ (c1 - c3, c1 + c3 + c5)
(x2, y2) = ½ (c2 - c4, c2 + c4 - c5)
Aplicando este procedimento à resolução do problema acima, obtém-se: c1 = 17, c2 = 30, c3 = -10, c4 = 9 e c5 = 19.
Os hipermercados mais afastados ficam à distância rectilinear de c5 / 2 = 9,5 do centro de distribuição, cuja localização óptima é em qualquer ponto do segmento de recta L que une os pontos: (x1, y1) = (13,5; 13) e (x2, y2) = (10,5; 10) (Francis et al., 1992 e Marco, 2006g).
Suponha-se que existem cinco hipermercados localizados nos pontos (0, 0), (0, 10), (20, 0), (40, 10) e (10, 10). Estes hipermercados necessitam de ser abastecidos com frequências esperadas de 6, 10, 11, 12 e 5 vezes por mês, respectivamente. O custo do abastecimento é de 10 UM por unidade de distância. O custo mensal de posse e operação de um centro de distribuição é de 6 000 UM. As distâncias apropriadas são rectilineares e um hipermercado é abastecido só por um centro de distribuição.
Para um centro de distribuição, n = 1, a localização de um único centro de distribuição é facilmente determinada usando a propriedade mediana. O total dos pesos é 44 e (x*, y*) = (20, 10); a distância total percorrida é de 780 (num sentido); portanto
ψn = 1 = 10 (2) (780) + 6 000, ou seja , 21 600 UM
Com n = 2, existem
S (2, 5) = ∑ [(-1)k (2 – k)5 / k! (2 - k!)], para k = 0, ..., (n - 1) = 15
combinações de afectação para serem consideradas. Normalmente, todavia, algumas combinações podem ser eliminadas por inspecção devido à topografia da situação.
Uma heurística que pode ser utilizada para reduzir o número de cáculos envolvidos é eliminar combinações de afectação que resultam em regiões a abastecer pelos novos centros de distribuição que se intersectam.
Para n = 2, a afectação de um novo centro de distribuição aos hipermercados 3 e 4 resulta em regiões a abastecer, representadas na Figura 5.18, que não se intersectam. Como se mostra na Figura 5.18, para distâncias rectilineares, uma região a abastecer é definida como sendo o menor rectângulo contendo os hipermercados a serem abastecidos pelo novo centro de distribuição.
 Figura 5.18. Regiões de abastecimento para a combinação de afectação
Figura 5.18. Regiões de abastecimento para a combinação de afectaçãode um novo centro de distribuição aos hipermercados 3 e 4
(carregar com o cursor na figura para ver em tamanho grande)
Neste caso, são eliminadas onze combinações de afectação com regiões de abastecimento que se intersectam. Os resultados para as restantes quatro combinações são resumidos na Tabela 5.4. A afectação óptima é um novo centro de distribuição abastecer o hipermercado 4 e o outro novo centro de distribuição abastecer os hipermercados restantes; o custo resultante é ψ*n = 2 = 20 400 UM.
| Combinação | Hipermercados afectados ao novo centro de distribuição 1 | (x1*, y1*) | (x2*, y2*) | ψn = 2 |
| 4 | 4 | (40, 10) | (0, 0) | 20 400 |
| 6 | 1, 2 | (0, 10) | (20, 10) | 21 200 |
| 7 | 1, 3 | (20, 0) | (10, 10) | 23 600 |
| 13 | 3, 4 | (40, 10) | (0, 10) | 20 800 |
Para n = 3, existem
S (3, 5) = ∑ [(-1)k (3 – k)5 / k! (3 - k!)], para k = 0, ..., (n - 1) = 25
combinações de afectação para serem consideradas. Neste caso, são eliminadas 16 combinações de afectação com regiões de abastecimento que se intersectam. Os resultados para as restantes nove combinações são resumidos na Tabela 5.5. A afectação óptima é um centro de distribuição abastecer o hipermercado 3, outro centro de distribuição abastecer o hipermercado 4 e o terceiro centro de distribuição abastecer os hipermercados 1, 2 e 5. O custo total dessa afectação é ψ*n = 3 = 20 200 UM.
| Hipermercados afectados ao novo centro de distribuição | |||||||
| Combinação | 1 | 2 | 3 | (x1*, y1*) | (x2*, y2*) | (x3*, y3*) | ψn = 3 |
| 1 | 1 | 2 | 3, 4, 5 | (0, 0) | (0, 10) | (20, 10) | 26 000 |
| 2 | 1 | 3 | 2, 4, 5 | (0, 0) | (20, 0) | (10, 10) | 27 200 |
| 8 | 3 | 4 | 1, 2, 5 | (20, 0) | (40, 10) | (0, 10) | 20 200 |
| 13 | 1 | 2, 5 | 3, 4 | (0, 0) | (0, 10) | (40, 10) | 25 600 |
| 16 | 2 | 4, 5 | 1, 3 | (0, 10) | (40, 10) | (20, 0) | 23 400 |
| 17 | 3 | 1, 2 | 4, 5 | (20, 0) | (0, 10) | (40, 10) | 22 200 |
| 20 | 4 | 1, 2 | 3, 5 | (40, 10) | (0, 10) | (20, 0) | 21 200 |
| 21 | 4 | 1, 3 | 2, 5 | (40, 10) | (20, 0) | (0, 10) | 21 400 |
| 23 | 5 | 1, 2 | 3, 4 | (10, 10) | (0, 10) | (40, 10) | 25 800 |
Para n = 4, existem
S (4, 5) = ∑ [(-1)k (4 – k)5 / k! (4 - k!)], para k = 0, ..., (n - 1) = 10
combinações de afectação a considerar. Uma vez que o custo dos novos centros de distribuição é de 24 000, é, no entanto, óbvio que ψ*n = 4 > ψ*n = 3. Da mesma forma, para n = 5, ψ*n = 5 > ψ*n = 3. Portanto, conclui-se que n* = 3, (x1*, y1*) = (20, 0), (x2*, y2*) = (40, 10) e (x3*, y3*) = (0, 10) (Tompkins e White, 1984 e Santos, 2006h).
Neste caso, pretende-se localizar um tapete transportador num centro de distribuição onde serve n pontos de carga e/ou descarga com um peso associado, positivo.
O problema é localizar o tapete x2 = A* + S* x1, tal que a soma das distâncias ponderadas perpendiculares ao tapete (o custo total do sistema) seja minimizada.
A distância perpendicular dos pontos de carga e/ou descarga (aj 1, aj 2) ao tapete é:
|A - (aj 2 - S aj 1)| / (S2 + 1)1/2
o que implica o problema de localização:
minimizar P (A, S) = ∑ [wj |A - (aj 2 - S aj 1| / (S2 + 1)1/2]
Duas simplificações, são sugeridas:
1) A localização óptima do tapete tem que passar, no mínimo, por dois pontos de carga e/ou descarga. Neste caso pode ser seguida uma abordagem simples de busca. Calculam-se, simplesmente, as intersecções A e declives S das n (n - 1) / 2 linhas que passam por todos os pares de pontos, calcula-se o valor da função objectivo e escolhe-se a localização óptima do tapete.
2) O algoritmo de resolução pode ser visto como rodando o tapete, usando ponto pivot após ponto pivot tais que a localização do tapete continue a ser mediana. Isto é fácil de fazer graficamente, para problemas pequenos.
Suponha-se que existem quatro pontos de carga e/ou descarga cujas coordenadas e pesos, wi, são dados na Tabela 5.6.
| j | wi | aj 1 | aj 2 |
| 1 | 2 | 1 | 5 |
| 2 | 1 | 4 | 4 |
| 3 | 1 | 6 | 6 |
| 4 | 1 | 3 | 4 |
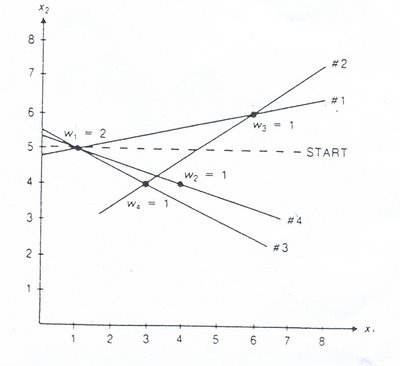
A Figura 5.19 ilustra o procedimento de rotação. Começando com o tapete horizontal, ele tem que passar pelo ponto 1 para dividir os pesos por dois. Esta localização, contudo, intercepta apenas um ponto e não pode ser óptima. Roda-se, portanto, o tapete no sentido contrário ao dos ponteiros do relógio com o ponto 1 como pivot até se obter a localização #1 da Figura 5.19. Para esta localização continuar mediana, o ponto 3 torna-se o pivot até que a localização #2 é produzida. Depois, o ponto 4 torna-se o pivot até que a localização #3 é produzida. O ponto 1 torna-se então o pivot para se criar a localização #4. Continua então a ser o pivot até o tapete estar de novo horizontal. Só quatro localizações precisam de ser avaliadas. Os índices dos pares de pontos de carga e/ou descarga são (1, 2), (1, 3), (1, 4) e (3,4). A Tabela 5.7 mostra as intercepções, (A), declive, (S), e o custo destas localizações. A localização que passa pelos pontos a1 e a2 é a óptima.
| Par | A | S | P (A, S) |
| (1, 2) | 16 / 3 | - 1 / 3 | 2,846 |
| (1, 3) | 24 / 5 | 1 / 5 | 2,942 |
| (1, 4) | 11 / 2 | - 1 / 2 | 3,578 |
| 3 / 4 | 2 | 2 / 3 | 4,438 |
(Love et al., 1984 e Santos, 2006m).
Suponha-se que 3 novos centros de distribuição, a, b e c, vão ser localizados numa região. Existem 6 hipermercados nessa região, p, q, r, s, t e u, que vão ser abastecidos por, pelo menos um dos novos centros de distribuição. Os hipermercados estão localizados em (0, 0), (0, 1), (0, 3), (1, 1), (2, 2) e (4, 0), respectivamente. Uma análise preliminar indica que existem cinco localizações possíveis, v, w, x, y e z, com coordenadas das localizações (1, 0), (1, 2), (2, 0), (4, 1) e (4,3), respectivamente, para os novos centros de distribuição. Os planos directores municipais, contudo, proíbem a localização do novo centro de distribuição a no local v e limitações de espaço impedem o novo centro de distribuição b de ser localizado em w. Não há trocas de mercadorias entre os três novos centros de distribuição.
A matriz W = (wi k), onde wi k é o número de viagens por dia feitas entre o novo centro de distribuição i e o hipermercado existente k, é
| wi k | p | q | r | s | t | u |
| a | 4 | 0 | 1 | 2 | 0 | 2 |
| b | 1 | 2 | 3 | 0 | 2 | 1 |
| c | 0 | 1 | 4 | 0 | 2 | 3 |
Todas as deslocações são supostas ocorrerem numa malha rectangular de estradas. A matriz das distâncias D = (dk j), onde dk j é a distância rectilinear entre o hipermercado existente k e a localização possível j, é dada por
| dk j | v | w | x | y | z |
| p | 1 | 3 | 2 | 5 | 7 |
| q | 2 | 2 | 3 | 4 | 6 |
| r | 4 | 2 | 5 | 6 | 4 |
| s | 1 | 1 | 2 | 3 | 5 |
| t | 3 | 1 | 2 | 3 | 3 |
| u | 3 | 5 | 2 | 1 | 3 |
A matriz dos custos C = (ci j), onde ci j é custo de localizar o novo centro de distribuição i na localização possível j, é obtida por C = W D
| ci j | v | w | x | y | z |
| a | 16 | 26 | 21 | 34 | 48 |
| b | 26 | 20 | 29 | 38 | 40 |
| c | 33 | 27 | 33 | 37 | 37 |
Note-se que ci j = ∑ wi k dk j, é uma soma de distâncias ponderadas.
Recorde-se que os novos centros de distribuição a e b não são permitidos nas localizações v e w, respectivamente. Para evitar a possibilidade destas afectações, fazem-se os valores de c1 1 e c2 2 positivos muito grandes. Atendendo a que os novos centros de distribuição a serem localizados são menos do que os locais disponíveis, são criadas dois novos centros de distribuição artificiais, d e e, com ci j = 0, e a matriz de custos, C, passa a ser
| ∞ | 26 | 21 | 34 | 48 |
| 26 | ∞ | 29 | 38 | 40 |
| 33 | 27 | 33 | 37 | 37 |
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 |
Este problema de afectação, em particular, pode ser resolvido por inspecção, resultando na afectação dos novos centros de distribuição a, b e c aos locais x, v e w, respectivamente, de modo a minimizar a distância percorrida por dia.
Claro que nem todos os problemas de afectação são tão fáceis de resolver como neste caso. Os métodos para resolver problemas de afectação são apresentados na maior parte dos textos introdutórios de investigação operacional.
Para além dos custos referidos acima, podem existir custos adicionais, resultantes da localização do novo centro de distribuição i no local j, tais como custos de preparação ou aquisição do terreno. Se c"i j denotar a soma destes outros custos e c'i j representar os custos referidos acima, então os valores dos custos ci j a usar na resolução do problema de afectação são dados por
ci j = c'i j + c"i j
Naturalmente, c'i j e c"i j têm que ter as mesmas dimensões (Francis e White, 1974 e Santos, 2006j).
Quando há trocas de mercadorias ou materiais entre as novas instalações, o problema é de afectação quadrática.
Suponha-se que queremos localizar quatro postos de trabalho, no talho de um hipermercado. Os valores dos fluxos e distâncias são dadas nas matrizes simétricas V e D,
| V | = | 0 | 2 | 8 | 3 |
| 2 | 0 | 4 | 9 | ||
| 8 | 4 | 0 | 5 | ||
| 3 | 9 | 5 | 0 |
| D | = | 0 | 8 | 10 | 2 |
| 8 | 0 | 4 | 7 | ||
| 10 | 4 | 0 | 9 | ||
| 2 | 7 | 9 | 0 |
Ordenando os valores de vj h e os valores dk l obtêm-se os vectores v e d.
v = (9, 8, 5, 4, 3, 2)
e
d = (2, 4, 7, 8, 9, 10)
O limite inferior LB é dado por
LB = v d’ = 9 (2) + 8 (4) + 5 (7) + 4 (8) + 3 (9) + 2 (10) = 164
Procedimento de Construção
O maior valor de fluxo (v2 4 = 9) é entre os postos de trabalho 2 e 4; a menor distância (d1 4 = 2) é entre os locais 1 e 4. Então, o posto de trabalho 1 é afectado ou ao local 1 ou local 4 e o posto de trabalho 4 é afectado ao local restante. O valor seguinte de fluxo em v é v13 = 8 e o valor seguinte da distância em d é d2 3 = 4; portanto, é desejável afectar os postos de trabalho 1 e 3 aos locais 2 e 3. O valor seguinte de fluxo em v é v3 4= 5 e o valor seguinte da distância em d é d2 4 = 7; portanto, é desejável afectar os postos de trabalho 3 e 4 aos locais 2 e 4. Dado que o posto de trabalho 4 pode ser afectado ao local 1 ou local 4 e o posto de trabalho pode ser afectado ao local 2 ou local 4 ela, decorre que o posto de trabalho 4 é afectado ao local 4. Então, o posto de trabalho 2 é afectado ao local 1, o posto de trabalho 3 é afectado ao local 2 e o posto de trabalho 1 é afectado ao local 3.
O custo desta afectação é
z = v1 2 d3 1 + v1 3 d3 2 + v1 4 d3 4 + v2 3 d1 2 + v2 4 d1 4 + v3 4 d2 4
= 2 (10) + 8 (4) + 3 (9) + 4 (8) + 9 (2) + 5 (7)
= 164
Uma vez que o valor da função objectivo da afectação é igual ao limite inferior, foi obtida uma solução óptima. Isto nem sempre acontece. Para problemas maiores, os detalhes deste método tornam-se um pouco mais complicados; no entanto, o princípio mantém-se o mesmo: Localizar as instalações que têm a maior interacção (fluxo) o mais próximas possível (Tompkins et al., 1996 e Santos, 2006k).
Procedimento de Melhoria (Trocas de Pares)
Para o exemplo anterior, designe-se o locais numericamente e os postos de trabalho alfabeticamente. Os seguintes fluxos ocorrem entre os postos de trabalho: A B (2), A C (8), A D (3), B C (4), B D (9), e C D (5). Suponha-se que se começa afectando arbitrariamente postos de trabalho A, B, C e D aos locais 1, 2, 3 e 4, respectivamente;. Então, as distâncias entre os postos de trabalho são A B (8), A C (10), A D (2), B C (4), B D (7) e C D (9). O custo total resultante deste layout inicial é obtido somando o produto do fluxo pela distância de cada par de postos de trabalho. Portanto o custo total da solução inicial é
2 (8) + 8 (10) + 3 (2) + 4 (4) + 9 (7) + 5 (9) = 226.
Dada uma solução inicial, considere-se agora trocar as localizações entre pares de postos de trabalho. Suponha-se que A troca com B. Localizando B no local 1 e A no local 2 as novas distâncias são A B (8), A C (4), A D (7), B C (10), B D (2), e C D (9). O novo custo total é
2 (8) + 8 (4) + 3 (7) + 4 (10) + 9 (2) + 5 (9) = 172.
Não se faz já a troca A B, apesar de ser possível um redução do custo total. Vai-se calcular o custo total de todos os pares de trocas e então faz-se a troca de que resulta a maior redução no custo total.
A seguir, considera-se o efeito de trocar A com C, mas ainda com base na solução inicial. Da colocação de C no local 1 e A no local 3, resultam as seguintes distâncias: A B (4), A C (10), A D (9), B C (8), B D (7), e C D (2). O novo custo total é
2 (4) + 8 (10) + 3(9) + 4 (8) + 9 ( 7) + 5 (2) = 220.
O procedimento continua, considerando as trocas de A e D, B e C, B e D, e C e D. Os resultados das trocas são dados na Tabela 5.8 para a solução inicial. Como se pode verificar, a melhor troca, é entre C e D; então, a troca é feita para se obter a primeira solução melhorada.
| Distâncias | ||||||||
| Trocas de pares | ||||||||
| Fluxos | Pares de postos de trabalho | Solução inicial | A B | A C | A D | B C | B D | C D |
| 2 | A B | 8 | 8 | 4 | 7 | 10 | 2 | 8 |
| 8 | A C | 10 | 4 | 10 | 9 | 8 | 10 | 2 |
| 3 | A D | 2 | 7 | 9 | 2 | 2 | 8 | 10 |
| 4 | B C | 4 | 10 | 8 | 4 | 4 | 9 | 7 |
| 9 | B D | 7 | 2 | 7 | 8 | 9 | 7 | 4 |
| 5 | C D | 9 | 9 | 2 | 10 | 7 | 4 | 9 |
| Custo total | 226 | 172 | 220 | 230 | 222 | 227 | 171 | |
Seguidamente, considera-se o efeito no custo total de fazer troca de pares para a primeira solução melhorada. Os resultados das trocas são mostrados na Tabela 5.9. Como se pode ver, a maior redução no custo total ocorre quando os postos de trabalho C e D são trocados. Portanto, a troca é feita e obtém-se a segunda solução melhorada.
| Distâncias | ||||||||
| Trocas de pares | ||||||||
| Fluxos | Pares de postos de trabalho | Solução inicial | A B | A C | A D | B C | B D | C D |
| 2 | A B | 8 | 8 | 7 | 4 | 2 | 10 | 8 |
| 8 | A C | 2 | 7 | 2 | 9 | 8 | 2 | 2 |
| 3 | A D | 10 | 4 | 9 | 10 | 10 | 8 | 10 |
| 4 | B C | 7 | 2 | 8 | 7 | 7 | 9 | 7 |
| 9 | B D | 4 | 10 | 4 | 8 | 9 | 4 | 4 |
| 5 | C D | 9 | 9 | 10 | 2 | 4 | 7 | 9 |
| Custo total | 171 | 227 | 175 | 220 | 227 | 167 | 226 | |
Normalmente, o processo continua sendo consideradas as trocas de pares para a segunda solução melhorada. A procura da melhor solução termina quando não há trocas que resultem numa redução do custo total ou o limite inferior é obtido. Neste caso, não há trocas que resultem numa redução do custo total.
Santos, 2006l).
Suponha-se que existem cinco locais potenciais, A, B, C, D e E, para a construção de novos centros de distribuição para abastecerem os hipermercados localizados nas cidades 1, 2, 3, 4, 5. Para cada local, os custos anuais de abastecer um hipermercado são dados na Tabela 5.10. O custo fixo anual de dispôr de um centro de distribuição também é dado para cada local.
| Locais para centros de distribuição | |||||
| Localização de | |||||
| hipermercados | A | B | C | D | E |
| 1 | 100 | 500 | 1 800 | 1 300 | 1 700 |
| 2 | 1 500 | 200 | 2 600 | 1 400 | 1 800 |
| 3 | 2 500 | 1 200 | 1 700 | 300 | 1 900 |
| 4 | 2 800 | 1 800 | 700 | 800 | 800 |
| 5 | 10 000 | 12 000 | 800 | 8 000 | 900 |
| Custos fixos | 3 000 | 2 000 | 2 000 | 3 000 | 4 000 |
Se apenas for construído um centro de distribuição, a selecção do local A resulta num custo total anual de 19 900 UM, incluindo o custo do novo centro de distribuição. Os custos totais anuais dos restantes locais são: 17 700, 9 600, 14 800 e 11 100 UM. Portanto, deve ser seleccionado o local C. Note-se que se se localizar um centro de distribuição em C, então os hipermercados das cidades 4 e 5 são sempre abastecidos pelo centro de distribuição no local C, independentemente de quaisquer decisões subsequentes de localizar novos centros de distribuição noutros locais.
Suponha-se que se decide localizar um novo centro de distribuição em A, juntamente com o centro de distribuição no local C.
Os hipermercados localizados nas cidades 1 e 2 são abastecidos do local A com uma poupança de 1 700 + 1 100 = 2 800 UM, o que é menos que o custo fixo de 3 000 UM de dispôr de um novo centro de distribuição em A. Localizando um novo centro de distribuição em B resulta numa redução de custos de 1 300 + 2 400 + 500 = 4 200 para os hipermercados localizados nas cidades 1, 2 e 3; dado que a redução de custos excede em 2 200 UM o custo fixo de 2 000, o local B é um candidato viável para um centro de distribuição adicional. Localizando um novo centro de distribuição em D resulta numa economia anual de 3 100 UM, ultrapassada pelo custo fixo anual de 3 000 UM. O local E resulta numa economia anual de 100 UM para o hipermercado localizado na cidade 1 a um custo fixo de 4 000 UM. Um segundo centro de distribuição vai ser localizado em B uma vez que a maior poupança líquida anual ocorre no local B. O novo custo total anual é (9 600 – 4 200) + 2 000 = 7 400.
Nesta altura, localizaram-se novos centros de distribuição em B e C. Adicionando um terceiro, as poupanças anuais líquidas resultantes da localização do terceiro centro de distribuição em j, designada por NAS (j), são
NAS (A) = 400 – 300 = - 2 600 UM
NAS (D) = 900 – 3 000 = - 2 100 UM
NAS (E) = 0 – 4 000 = - 4 000 UM
Portanto, não se justifica nenhum centro de distribuição adicional e os novos centros de distribuição são localizados somente em B e C, a um custo total anual de 7 400 UM. O centro de distribuição localizado em C abastece os hipermercados localizados nas cidades 4 e 5 e o centro de distribuição localizado em B abastece os hipermercados localizados nas cidades 1, 2 e 3.
A abordagem de continuar a adicionar centros de distribuição em locais com as maiores economias líquidas anuais não garante que resulte numa solução óptima. Em particular, pode acontecer que uma adição subsequente de centros de distribuição faz com que alguma decisão anterior de adicionar um centro de distribuição não seja óptima. Uma abordagem que pode ser usada para obviar parcialmente essa possibilidade é retirar da solução o local que produz a maior economia anual. Uma verificação de «eliminações» viáveis é feita depois de cada verificação de «adicções» viáveis (Tompkins et al., 1996 e Santos, 2006g).


0 Comments:
Post a Comment
<< Home