V. Planeamento e Projecto de Hipermercados (Continuação)
Localização numa Rede em Árvore
O novo centro de distribuição pode abastecer os hipermercados localizados nos nós ou o novo hipermercado abastecer centros populacionais. A nova instalação deve ser localizada de modo a minimizar a distância total percorrida, durante um determinado período, entre a nova localização e as existentes.
Designando wi como sendo o número de deslocações de ida e volta, o custo de transporte ou o tempo de deslocação por unidade de distância, por unidade de tempo, entre o ponto x e o vértice vi, o objectivo é minimizar:
Este problema tem algumas características que convém salientar. Uma delas é que pelo menos um vértice é uma localização óptima ou mediana absoluta. Só os vértices precisam de ser considerados como localizações potenciais.
Outra propriedade importante é que a localização mediana depende dos pesos, wi, e da estrutura da árvore, mas não das distâncias entre os nós. É claro que o valor de f(x) depende das distâncias entre os nós.
Outra, ainda, é que uma sub-árvore que contenha pelo menos metade dos pesos, contém a localização mediana
Algoritmo para Determinar a Mediana
1) Escolher uma ponta qualquer vt com peso wt. Se wt for maior ou igual a W / 2 (metade da soma dos pesos), essa ponta é a mediana e parar.
2) Designar por va o nó adjacente a vt; adicionar wt a wa para obter o novo peso para va. Apagar da árvore todos os pontos do arco [vt, va], excepto va, e voltar ao passo 1.
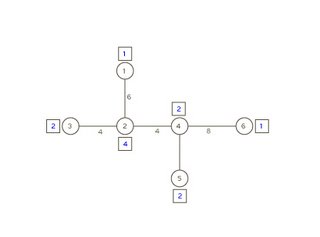
Para determinar a localização mediana de um hipermercado, na árvore da Figura 5.2, comece-se por escolher uma ponta, por exemplo, v1.
(carregar com o cursor na figura para ver em tamanho grande)
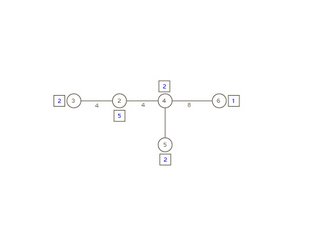
Como o peso de v1 é inferior a W / 2 = 6, adiciona-se o peso de v1 ao peso do vértice adjacente v2 e apaga-se v1 e o caminho que o liga a v2 (Figura 5.3).
(carregar com o cursor na figura para ver em tamanho grande)
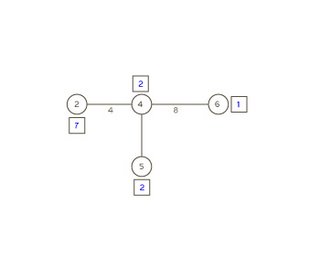
Escolhendo v3, como o peso de v3 é inferior a W / 2 = 6, adiciona-se o peso de v3 ao peso do vértice adjacente v2 e apaga-se v3 e o caminho que o liga a v2 (Figura 5.4).
Como o peso de v2 é maior que W / 2 = 6, v2 é a localização mediana.
(carregar com o cursor na figura para ver em tamanho grande)
O valor óptimo da função objectivo é dado por:
f(x*) = 1 × 6 + 2 × 4 + 2 × 4 + 2 × 10 + 1 × 12 = 54
(Marco, 2006h).
O objectivo é localizar um novo centro de distribuição, hipermercado ou outra instalação num ponto y*, de uma rede em árvore, que minimize o máximo das distâncias ponderadas entre a nova instalação e um conjunto de hipermercados, centros populacionais ou outros, localizados nos nós da árvore, vi. Esse ponto designa-se por centro absoluto.
A nova instalação deve ser localizada de modo a minimizar um tempo, custo ou perda: a preocupação é com o pior caso que se quer tornar no menor mal possível.
Se g(y) fôr o máximo das distâncias ponderadas entre y e os nós da árvore, tem-se:
O centro absoluto y* é um ponto na árvore que minimiza g (y). O centro absoluto não ponderado localiza-se a meio do caminho mais longo da árvore, de onde se poder usar o algoritmo particularmente simples, seguinte, para resolver o problema.
Algoritmo para Determinar o Centro Absoluto Não-Ponderado
1) Escolher um nó qualquer, v.
2) Encontrar uma ponta da árvore, v', que esteja o mais afastada de v (por exemplo, v3).
3) Encontrar uma ponta da árvore, v", que esteja o mais afastada de v' (por exemplo, v1). O ponto a meio do caminho que liga v' a v" é o único centro absoluto.
Para determinar a localização central de um centro de distribuição, na árvore da Figura 5.5, comece-se por escolher, por exemplo, v1. v3 é a ponta da árvore mais afastada de v1. v1 é a ponta da árvore mais afastada de v3. Então o centro absoluto, y* localiza-se no arco (v2, v3), a uma unidade de distância de v2.

(carregar com o cursor na figura para ver em tamanho grande)
Fonte: Francis et al. (1992)
O valor óptimo da função objectivo é g(y*) = 5
(Marco, 2006i).
Procedimento para Determinar o Centro Absoluto Ponderado
Primeiro calcule-se bs t. Então y* é o ponto único no caminho que liga os nós s e t que satisfaz as seguintes equações:
d (y*, vt)= ws d (vs, vt) / ( ws + wt)
com
e
Portanto, bs t é o menor valor de z, que, por sua vez, é o menor valor da função objectivo do problema do centro absoluto.
Com
para calcular bs t, o maior valor da matriz B = (bi j), o procedimento é o seguinte:
1) Calcular os valores de uma linha qualquer de B, por exemplo l (1), e encontrar o maior valor na linha l (1), por exemplo na coluna c (1).
2) Calcular os valores da coluna c (1) e encontrar o maior valor na coluna c (1), que ocorre, por exemplo, na linha l (2).
3) Calcular os valores da linha l (2), e encontrar o maior valor na linha l (2) e assim sucessivamente, continuando até se encontrar, pela primeira vez, a mesma entrada da matriz duas vezes seguidas; este número será o maior elemento da matriz B.
Considere-se, por exemplo, a rede em árvore da Figura 5.6, onde os nós representam localizações de hipermercados e os pesos, tempo por unidade de distância.

Fonte: Francis et al. (1992)
Para determinar a localização de um novo centro de distribuição que minimize o tempo máximo das viagens de entregas aos hipermercados, o centro absoluto da rede em árvore da Figura 5.6, pode-se ver que o maior valor da matriz B (Figura 5.7) é b3 5 = 14. Portanto, o tempo máximo para fazer uma entrega, g (y*), é 14. Para determinar a localização do centro de distribuição, y*, utilizam-se as equações acima e, uma vez que w3 = w5 = 2, conclui-se que o centro de distribuição,y*, deve ficar a meio do caminho entre os hipermercados 3 e 5, v3 e v5, ou seja, no arco (v2, v4), a três unidades de distância do hipermercado 2, v2 (Marco, 2006j).

Fonte: Francis et al. (1992)
Interpretando wi d (y, vi) como o tempo do transporte de y para o nó i, pode-se designar por adenda, hi, o tempo de preparar o transporte mais o tempo de carga ou descarga no nó, mais o tempo de viagem do nó i para qualquer outro ponto conhecido na rede, tal como um centro de recolha de veículos. Naturalmente, dependendo das circunstâncias, alguns destes tempos podem ser nulos.
Neste caso, a função g (y) que se pretende minimizar é
g (y) = max {w1 d (y, v1) + h1, …,wm d (y, vm) + hm}
Procedimento para Determinar o Centro Absoluto Ponderado com Adendas
1) Para cada i e j tais que 1 ≤ i < j ≤ m, calcular bi j, agora definido como sendo
bi j = (wi wj d (vi, vj) + wj hi + wi hj) / (wi + wj)
e depois calcular bs t, definido, como sendo o máximo de bi j.
2) Calcular hp, definido como sendo o máximo dos hi.
3) Calcular b, definido como sendo o máximo de bs t e hp.
4) Se b = hp, então y* = vp, é o único centro absoluto e o problema está resolvido.
5) Se não, quando b = bs t, então y*, é o ponto único, no caminho que liga os vértices s e t, que satisfaz
d (y*, vs) = (wt d (vs, vt) + ht – hs) / (ws + wt)
d (y*, vt) = (ws d (vs, vt) + hs – ht) / (ws + wt)
Procedimento para Determinar o Centro Absoluto Ponderado num Nó
Tendo utilizado o procedimento para determinar o centro absoluto ponderado y*, para resolver o problema do centro absoluto ponderado num nó (se y* não é um nó) só é necessário avaliar g nos nós do arco que contém y* e escolher como centro absoluto ponderado num nó um dos dois nós com o menor valor de g.
Para o exemplo anterior, uma vez que y* é no arco que une os nós 2 e 4, também se pode concluir que ou o nó 2 ou o nó 4 é o centro absoluto ponderado num nó. Os cálculos estabelecem que g (v2) = 20 e que g (v4) = 16, portanto o nó 4 é o centro absoluto ponderado num nó (Marco, 2006m).
O objectivo é localizar o menor número de novos centros de distribuição, hipermercados ou outras instalações, em vários pontos de uma rede em árvore, de modo a que não seja ultrapassada uma certa distância si, entre cada nó i da árvore e a instalação nova mais próxima. As novas instalações chamam-se centros. Esses centros prestam serviços, por exemplo, de abastecimento ou distribuição, aos nós da árvore, onde se localizam, por exemplo, hipermercados ou centros populacionais. As novas localizações ser localizadas em qualquer ponto da árvore.
Considere-se o caso da Figura 5.8a em que cada nó representa um hipermercado. As linhas sinuosas ligadas aos nós 1 a 5 são fios cujos comprimentos são os limites superiores das restrições de cobertura, portanto. s1 = 10, s2 = 5 e assim por diante. Qualquer centro de distribuição x cuja localização na árvore satisfaça d (x, vi) ≤ si diz-se que cobre o nó (hipermercado) i. Pelo menos um centro tem que estar a uma distância menor que 10 do hipermercado 1, menor que 5 do hipermercado 2 e assim por diante; isto é, pelo menos um centro tem que cobrir cada hipermercado.

(carregar com o cursor na figura para ver em tamanho grande)
Fonte: Francis et al., 1992
Escolhe-se uma das pontas da árvore, por exemplo v4, e verifica-se se o fio de comprimento 14 (se não houver um fio na ponta escolhida, a ponta e o arco com esse nó podem ser apagados da árvore) chega ao nó adjacente à ponta, v6 à distância de 10. O fio chega a v6, por isso, remove-se o arco com o nó v4 e fica-se com um fio com o comprimento restante 14 - 10 = 4 (Figura 5.8b) ligado a v6.
Continua-se a escolher uma ponta da árvore, por exemplo v5, e verifica-se se o fio de comprimento 15 chega ao nó adjacente à ponta, v6. O fio chega a v6, por isso, remove-se o arco com o nó v5 e fica-se com um fio com o comprimento restante 15 - 12 = 3 ligado a v6. Agora há dois fios ligados a v6. Nestes casos o fio de maior comprimento é removido do modelo. Fica, portanto, um fio de comprimento 3 ligado a v6 (Figura 5.8c).
Suponha-se que a ponta escolhida a seguir é v6 com um fio de comprimento 3. Como este fio não chega a v2 localiza-se um centro num ponto y1, no arco que liga os nós 2 e 6, a uma distancia de 3 de v6 e remove-se todo o arco do modelo (Figura 5.8d). Dado que o fio com origem em v5 é que fez com que o centro 1 fosse localizado, regista-se o facto de v5 ser um nó distinto, u1 = {v5}. Determina-se, também, se algum dos fios restantes na árvore chegam a y1, para que os nós que lhes estão ligados possam ser cobertos pelo centro. Neste caso, nenhum fio restante na árvore chega a y1. O centro que se localizou cobre ambos os hipermercados 4 e 5.
Suponha-se que a seguir se escolhe o vértice v1 como ponta da árvore restante: o fio de v1 não chega a v2, por isso localiza-se um segundo centro em y2, no arco que liga os vértices 1 e 2, à distancia de 10 de v1. O fio de v2 chega a y2, por isso é removido. Regista-se o facto de v1 ser um vértice distinto. Remove-se a parte do arco (v1, v2) de v1 a y2 e y2 torna-se uma ponta da árvore sem fio. Por isso, na próxima iteração, pode-se omitir o arco que liga y2 a v2 (Figura 5.8e).
Neste ponto a árvore restante tem apenas um único arco ligando v2 a v3 com um fio de comprimento 3 em v3: este fio não chega a v2, por isso localiza-se um terceiro centro em y3, no arco que liga os vértices 2 e 3, à distância de 3 de v3. Não restam mais fios no modelo, por isso não há necessidade de verificar se algum outro fio chega a y3. Regista-se o facto de v3 ser um vértice distinto. Removendo o arco que liga os vértices 2 e 3, fica-se com um único nó, v2, sem fios ligados (Figura 5.9f).
O procedimento termina, tendo-se localizado três centros, nos pontos y1, y2 e y3, a solução óptima para o problema, e identificado três nós distintos, v1, v3 e v5 (Marco, 2006k).


0 Comments:
Post a Comment
<< Home