V. Planeamento e Projecto de Hipermercados (Continuação)
Distâncias Rectilineares
X = (x, y), localização do novo centro de distribuição
Hi = (ai, bi), localização do hipermercado existente i, i = 1, 2, …, m.
O custo anual das deslocações entre o novo centro de distribuição e o hipermercado existente i é suposto ser proporcional à distância entre os pontos X e Hi, com wi a denotar a constante de proporcionalidade. O objectivo é determinar o valor de X que minimize a soma ponderada das distâncias percorridas, o custo anual das deslocações:
onde:
d (X, Hi), é a distância entre os pontos X e Hi e wi é o «peso» entre o novo centro de distribuição e o hipermercado existente i.
Considerando que as distâncias apropriadas são rectilineares, tem-se:
e o problema da localização minisoma é:
Dado que nesta equação os termos envolvendo x são separados dos que envolvem y, é possível determinar os valores óptimos de x e y independentemente.
Outras duas importantes propriedades deste problema são:
1) a coordenada óptima x* da nova instalação é igual à coordenada x de alguma das instalações existentes; e
2) a coordenada óptima x* não tem mais do que metade do total dos pesos para cada lado;
o mesmo acontecendo com a coordenada óptima y*.
A determinação da solução óptima deste problema pode ser ilustrada considerando o caso envolvendo a localização de um novo centro de distribuição. Há cinco hipermercados que vão ser servidos pelo novo centro de distribuição, localizados nos pontos H1 = (1, 1), H2 = (5, 2), H3 = (2, 8), H4 = (4, 4) e H5 = (8, 6). O custo por unidade de distância é o mesmo entre o novo centro de distribuição e cada um dos hipermercados existentes. O número de viagens por dia entre o novo centro de distribuição e os hipermercados existentes será 5, 6, 2, 4 e 8, respectivamente.
Ordenando as coordenadas x dos hipermercados existentes, dá a sequência de hipermercados 1, 2, 4, 5 e 8, com a correspondente sequência de pesos de 5, 2, 4, 6, e 8. O peso total é 25. Como se pode ver na Tabela 5.1, a soma parcial dos pesos iguala ou excede metade do total com i = 2; portanto x* = a2 = 5. Se a soma parcial for igual a metade da soma de todos os pesos, então a solução inclui todos os pontos entre a coordenada para a qual a igualdade ocorreu e o valor da coordenada seguinte. De forma semelhante, como se apresenta na Tabela 5.2, a coordenada óptima de y é y* = b4 = 4. Então a localização óptima do novo centro de distribuição é X* = (5, 4), como se mostra na Figura 5.10.
| Hipermercado | Coordenada | Peso | ∑ wi |
| i | ai | wi | |
| 1 | 1 | 5 | 5 |
| 3 | 2 | 2 | 7 |
| 4 | 4 | 4 | 11 < 25 / 2 |
| 2 | 5 | 6 | 17 > 25 / 2 |
| 5 | 8 | 8 | 25 |
Tabela 5.2. Solução para a coordenada y
| Hipermercado | Coordenada | Peso | ∑ wi |
| i | bi | wi | |
| 1 | 1 | 5 | 5 |
| 2 | 2 | 6 | 11 < 25 / 2 |
| 4 | 4 | 4 | 15 > 25 / 2 |
| 5 | 6 | 8 | 23 |
| 3 | 8 | 2 | 25 |

A distância ponderada total, resultante da localização X* = (5, 4) é obtida como se segue:
f (5, 4) = 5 (|5 - 1| + |4 - 1|) + 6 (|5 - 5| + |4 - 2|) + 2 (|5 - 2| + |4 - 8|) + 4 (|5 - 4| + |4 - 4|) + 8 (|5 - 8| + |4 - 6|) = 105 unidades de distância.
Se não for possível localizar o novo centro de distribuição no ponto (5, 4), podem ser avaliados locais alternativos calculando o valor de f (X) para cada local e seleccionando o local com o menor valor de f (X) (Tompkins et al., 1996 e Santos, 2006d).
Na situação anterior, suponha-se que só é possível localizar o novo centro de distribuição nos seguintes locais alternativos: L1 = (5, 6), L2 = (4, 2) e L3 = (8, 4). Calculando o valor da função objectivo f (X) para X = Lk, k = 1, 2, 3 tem-se
f (5, 6) = 5 (|5 - 1| + |6 - 1|) + 6 (|5 - 5| + |6 – 2|) + 2 (|5 - 2| + |6 - 8|) + 4 (|5 - 4| + |6 - 4|) + 8 (|5 - 8| + |6 - 6|) = 115
f (4, 2) = 5 (|4 - 1| + |2 - 1|) + 6 (|4 - 5| + |2 – 2|) + 2 (|4 - 2| + |2 - 8|) + 4 (|4 - 4| + |2 - 4|) + 8 (|4 - 8| + |2 - 6|) = 114
f (8, 4) = 5 (|8 - 1| + |4 - 1|) + 6 (|8 - 5| + |4 – 2|) + 2 (|8 - 2| + |4 - 8|) + 4 (|8 - 4| + |4 - 4|) + 8 (|8 - 8| + |4 - 6|) = 132
Então, o melhor local seria L2; no entanto, L1 tem quase o mesmo valor de f (X). Considerações qualitativas, assim como considerações quantitativas não reflectidas em f (X), podem indicar que L1 é preferível a L2 (Santos, 2006e).
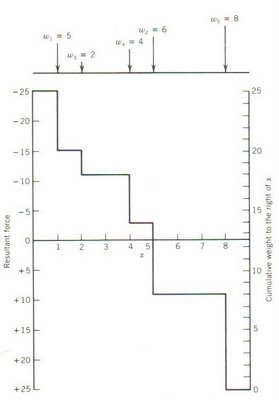
A analogia de wi a um peso pode ser extendida considerando os wi como sendo forças ao longo de uma viga. Para o exemplo anterior, considerando o eixo do x como sendo uma viga, resulta no diagrama de forças da Figura 5.11. Na vertical, do lado esquerdo, estão as resultantes das forças, para a direita negativas e para a esquerda positivas. Na vertical, do lado direito, estão os pesos acumulados à direita de x. Os pesos associados a cada hipermercado estão representados no topo do diagrama.
(carregar com o cursor na figura para ver em tamanho grande)
Se o novo centro de distribuição for localizado à esquerda de x = 1, existe uma força de - 25 a puxar o novo centro de distribuição para a direita. Para 1 < x < 2, há uma força de 5 puxando o novo centro de distribuição para a esquerda e uma força de 20 puxando o novo centro de distribuição para a direita; a força resultante de - 15 puxa o novo hipermercado para a direita. Para 2 < x < 4, há uma força resultante de - (4 + 6 + 8) + (5 + 2) = - 11, que puxa o novo centro de distribuição para a direita. Para 4 < x < 5, a força resultante é - 3; portanto, o novo centro de distribuição é puxado para a direita. Para 5 < x < 8, a força resultante é - 8 + (5 + 2 + 4 + 6) = + 9; portanto, o novo centro de distribuição é puxado para a esquerda. No diagrama de forças vê-se que a força resultante muda de sinal (-) para (+) quando x = 5; portanto x* = 5. A escala vertical à direita da Figura 5.11 mostra que a força resultante muda de sinal no mesmo valor de x que satisfaz a condição de optimalidade de não mais do que metade do peso total para a esquerda (direita) da localização da nova instalação. A mesma relação existe para a coordenada y.
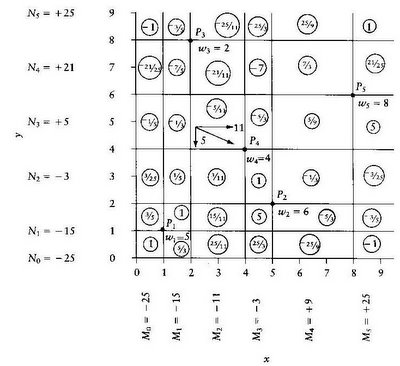
Na Figura 5.12, as forças resultante para o eixo dos x estão representadas por Mi e para o eixo dos y, por Nj. Por exemplo se o centro de distribuição for localizado em 2 < x < 4 e 4 < y < 6 há uma força de 11 para a direita e uma força de 5 para baixo. As forças para baixo são positivas e as forças para cima são negativas. A força resultante vai fazer com que o novo centro de distribuição seja puxado para baixo e para a direita, com a resultante das forças numa direcção com o declive de - 5 / 11; então, a força resultante Rij para uma dada região no plano é obtida dividindo o valor de Nj pelo valor de Mi indicados, ou
Rij = Nj / Mi
Note-se que Rij constitui o declive máximo ou a maior redução, para a função objectivo f (X). Na Figura 5.12, os valores de Rij são mostrados nas respectivas regiões.
(carregar com o cursor na figura para ver em tamanho grande)
Se em vez de se tentar mover na direcção da localização óptima, se quiser mover na direcção que não altere o valor da função objectivo, então move-se o novo centro de distribuição na direcção perpendicular à do declive máximo. Fazendo Sij denotar a direcção que não altera a função objectivo vê-se que
Si j = – 1 / Ri j = Mi / Nj
Os valores de Si j são os valores circundados na Figura 5.13. As linhas traçadas na Figura 5.13 têm declives iguais aos valores de Sij; então, estas são as linhas de isocusto ou de nível de f (X). Todos os pontos numa dada curva de nível têm o mesmo valor da função objectivo.

(carregar com o cursor na figura para ver em tamanho grande)
As curvas de nível podem ser usadas para orientar a procura de locais viáveis para o novo centro de distribuição se a solução «óptima» não é satisfatória por alguma razão (Santos, 2006f).
Distâncias Euclideanas ao Quadrado
Neste caso, assume-se que os custos crescem proporcionalmente ao quadrado da distância Euclideana (problema gravitacional).
Então, tem-se:
d (X, Hi) = [(x - ai)2 + (y - bi)2]
Sendo assim, o problema é formulado do seguinte modo:
Minimizar f (x, y) = ∑ wi [(x - ai)2 + (y - bi)2]
Os valores óptimos, x* e y*, que minimizam os custos, são obtidos igualando a zero as derivadas parciais da função objectivo em ordem a x e a y,
((∂f (x*, y*) / ∂x*), (∂f (x*, y*) / ∂y*)) = (0, 0)
de onde:
x* = ∑ wi ai / ∑ wi
y* = ∑ wi bi / ∑ wi
x* e y*, correspondem a médias ponderadas das coordenadas x e y das instalações existentes e são, de facto, as coordenadas que minimizam a equação dos custos. A solução do problema é algumas vezes designada de centróide ou centro de gravidade. Daí a designação de problema gravitacional.
Assim para o problema anterior,
x* = [5 (1) + 6 (5) + 2 (2) + 4 (4) + 8 (8)] / (5 + 6 + 2 + 4 + 8)
x* = 4,76
y* = [5 (1) + 6 (2) + 2 (8) + 4 (4) + 8 (6)] / (5 + 6 + 2 + 4 + 8)
y* = 3,88
O custo total, (f (X)*), resultante da localização X* = (4,76; 3,88) é então:
f (4,76; 3,88) = 5 [(4,76 - 1)2 + (3,88 - 1)2] + 6 [(4,76 - 5)2 + (3,88 – 2)2] + 2 [(4,76 - 2)2 + (3,88 - 8)2] + 4 [(4,76 - 4)2 + (3,88 - 4)2] + 8 [(4,76 - 8)2 + (3,88 - 6)2] = 305,2 UM
(Francis e White, 1974 e Prazeres, 2006a)
Pelas razões indicadas anteriormente para o problema rectilinear, são de interesse as curvas de nível do problema gravitacional. As curvas de nível do problema gravitacional podem ser obtidas muito facilmente. Considere-se as curvas de nível dadas na Figura 5.14 para dois casos simples do problema gravitacional. No primeiro caso existe uma instalação. No segundo caso existe igual movimento de artigos entre a instalação nova e cada uma de duas instalações existentes. Consequentemente, é fácil de ver que as curvas de nível serão circunferências concêntricas centradas na localização óptima.
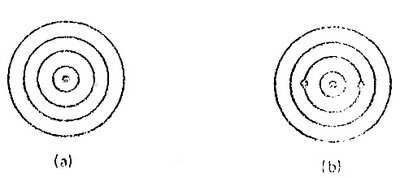
Agora, como é que se pensa que as curvas de nível serão quando se tem um número qualquer de instalações existentes com movimentação de artigos desigual? Se se suspeitou que as curvas de nível serão ainda circunferências concêntricas centradas na localização óptima, essa intuição é notável, pois é esse o caso. Para se ver porque isto é verdade, note-se que de expressão da função objectivo se quer determinar o conjunto de todos os pontos (x, y) tais que
k = ∑ wi [(x - ai)2 + (y - bi)2]
onde k é uma constante. Consequentemente, expandindo os termos quadrados determina-se que
k = x2 ∑ wi – 2 x ∑ wi ai + ∑ wi ai2 + y2 ∑ wi - 2 y ∑ wi bi + ∑ wi bi2
Se se fizer
W = ∑ wi
dividindo a equação anterior por W, e empregando as expressões de x* e y*, determina-se que
k / W = x2 - 2 x x* + ∑ (wi ai2) / W + y2 - 2 y y* + ∑ (wi bi2) / W
Adicionando (x*)2 e (y*)2 a ambos os lados da equação anterior e simplificando, obtém-se a equação de uma circunferência,
r2 = (x – x*)2 + (y – y*)2
centrada no ponto (x*, y*) com raio
r = [k / W + (x*)2 + (y*)2 - ∑ wi (ai2 + bi2) / W]1/2
Este é um resultado interessante e não intuitivo. Com base neste resultado, se não se puder localizar a nova instalação na localização óptima (x*, y*) e se tiver que avaliar locais alternativos, deve-se sempre escolher aquele que está a menor distância em linha recta do ponto (x*, y*).
Para o caso considerado anteriormente, tem-se:
r2 = (x – 4,76)2 + (y – 3,88)2
com
r = [k / 25 + (4,76)2 + (3,88)2 – 49,92]1/2
ou
r = [k / 25 -12,21]1/2, para k > 305,2 (o valor óptimo da função objectivo)
(Prazeres, 2006b).
Distâncias Euclideanas
Considerando que as distâncias apropriadas são Euclideanas, tem-se:
d (X, Hi) = [(x - ai)2 + (y - bi)2]1/2
e o problema da localização minisoma é:
Minimizar f (x, y) = ∑ wi [(x - ai)2 + (y - bi)2]1/2
Igualando a zero as derivadas parciais da função objectivo em ordem a x e a y, obtêm-se as expressões que dão o valor das coordenadas óptimas x* e y*,
x ∑ {wi / [(x - ai)2 + (y - bi)2]1/2} = ∑ {wi ai / [(x - ai)2 + (y - bi)2]1/2}
Fazendo gi (x, y) = wi / [(x - ai)2 + (y - bi)2]1/2,
obtém-se:
x = ∑ (ai gi (x, y)) / ∑ gi (x, y)
Analogamente, para y, tem-se:
y = ∑ (bi gi (x, y)) / ∑ gi (x, y)
Enquanto a equação gi (x, y) for definida, pode-se recorrer ao seguinte processo iterativo:
x(k + 1) = ∑ (ai gi (xk, yk)) / ∑ gi (xk, yk)
y(k + 1) = ∑ (bi gi (xk, yk)) / ∑ gi (xk, yk)
onde os expoentes representam o número da iteração.
O procedimento iterativo continua até que não ocorra uma melhoria significativa na estimativa da localização óptima da nova instalação.
Os valores iniciais do procedimento iterativo podem ser a solução do problema com distâncias rectlineares, Euclideanas ao quadrado, qualquer ponto do polígono definido pelas instalações existentes ou até mesmo a origem, desde que nenhuma destas alternativas coincida com a localização de uma instalação existente.
A utilização do procedimento iterativo para determinar a localização minisoma de um novo centro de distribuição (I), com os valores iniciais dados pela solução do problema com distâncias Euclideanas ao quadrado (x0 = 4,76 e y0 = 3,88), produz os seguintes resultados,
| k | xk | yk |
| 0 | 4,76 | 3,88 |
| 1 | 4,627 | 3,684 |
| 2 | 4,569 | 3,621 |
| 3 | 4,549 | 3,601 |
| 4 | 4,543 | 3,595 |
| 5 | 4,542 | 3,593 |
| 6 | 4,541 | 3,592 |
| 7 | 4,541 | 3,591 |
| 8 | 4,541 | 3,591 |
Na oitava iteração já não ocorre qualquer melhoria na estimativa da localização óptima do novo centro de distribuição, portanto (x*, y*) = (4,54; 3,59).
A distância ponderada total, resultante da localização X* = (4,54; 3,59) é então:
f* (4,54; 3,59) = 5 [(4,54 - 1)2 + (3,59 - 1)2]1/2 + 6 [(4,54 - 5)2 + (3,59 – 2)2]1/2 + 2 [(4,54 - 2)2 + (3,59 - 8)2]1/2 + 4 [(4,54 - 4)2 + (3,59 - 4)2]1/2 + 8 [(4,54 - 8)2 + (3,59 - 6)2]1/2 = 78,49
(Prazeres, 2006c).
A Falta de Dados para Abordagens Analíticas de Localização
Na resolução de problemas de localização, supôs-se que certos dados estão disponíveis. Concretamente, os valores de (ai, bi) e wi de cada instalação existente são supostos serem conhecidos. Nalguns casos, estes valores podem mudar ao longo do tempo. Noutros, os valores podem não ser conhecidos de todo. Se os valores mudam ao longo do tempo, pode-se estar interessado em minimizar o valor anual equivalente do custo das movimentações. Se os valores de (ai, bi) e wi não são conhecidos, sugere-se que sejam feitas diferentes estimativas desses valores e que o problema de localização seja resolvido para cada combinação de estimativas. Com base nas soluções obtidas e curvas de nível associadas, pode-se escolher a localização que melhor satisfaz os objectivos do problema em particular.
Muitas vezes, as abordagens analíticas não são usadas por causa da «falta de dados precisos». Esta é uma desculpa muito fraca por pelo menos duas razões. Primeiro, os modelos são, normalmente, bastante insensíveis a erros na estimativa dos valores dos parâmetros do modelo. Segundo, qual a abordagem alternativa que vai ser utilizada para tomar uma decisão? Sem dúvida, a abordagem alternativa baseia-se (pelo menos implicitamente) nas estimativas subjectivas dos valores dos parâmetros. Se é esse o caso, porque não explicitar essas estimativas e usar o modelo?
Se ainda não se quer atribuir valores aos parâmetros e, mesmo assim, é tomada uma decisão sobre a localização da nova instalação, então podem imputar-se valores ou intervalos de valores aos parâmetros. Para exemplificar, suponha-se que as suposições do problema gravitacional são satisfeitas e que existem três instalações localizadas em P1 = (0, 0), P2 = (2, 6) e P3 = (8, 4). Se for dito que não é possível estimar os valores de wi, mas que foi decidido localizar a nova instalação em (4, 4). Do que foi exposto anteriormente, para (x*, y*) ser igual a (4, 4) tem que ser verdade que
4 = 0 w1 + 2 w2 + 8 w3
4 = 0 w1 + 6 w2 + 4 w3
onde a escala de tempo foi escolhida de tal maneira que
1 = w1 + w2 + 4 w3
Consequentemente, tem-se um sistema de três equações com três incógnitas, que pode ser resolvido para se obter:
w1 = 0,2
w2 = 0,4
w3 = 0,4
Pode-se agora perguntar, «Espera-se ter, realmente, para a segunda instalação existente, duas vezes mais movimentações do que para a primeira e a mesma quantidade de movimentações entre a nova instalação e a segunda e terceira instalações existentes?» Se a resposta é «Não!», então devem ser especificados valores que são razoáveis para o problema de localização em causa. Podem ser seguidas abordagens semelhantes quando os modelos rectilineares e Euclideanos são apropriados. A análise, no entanto, não é tão simples como para o problema gravitacional (Prazeres, 2006d).
Modelo Gravitacional
Suponha-se que um grande retalhista está a considerar abrir um novo hipermercado no Centro Comercial do Parque. A concorrência tem dois hipermercados, um no Centro Comercial Cascata e outro no Cidadela.
Os quatro passos seguintes são repetidos para cada área envolvente do Centro Comercial do Parque, somando os resultados para obter o valor total estimado das vendas. Dado que um campus universitário próximo pode representar uma grande fonte potencial de clientes, descreve-se o processo de determinação da previsão de vendas, no hipermercado de cada centro comercial, à comunidade universitária.
Na Tabela 5.3 é dada a área de cada centro comercial e a respectiva distância à universidade.
| Centro Comercial | Área | Distância à universidade |
| - 10³ m² - | - km - | |
| Parque | 92,90 | 4,828 |
| Cascata | 46,45 | 8,047 |
| Cidadela | 9,29 | 1,609 |
- Determina-se a probabilidade de um membro da universidade fazer compras num centro comercial, usando a fórmula de Huff:
Pij = (Sj / Tijb) / Σ (Sj / Tijb),
onde,
Pij = probabilidade de uma pessoa com origem num determinado ponto i se deslocar a um determinado centro comercial j,
Sj = tamanho do centro comercial j,
Tij = tempo de deslocação ou distância do ponto de partida, i, das pessoas até ao centro comercial j,
b = expoente de Tij que reflecte o efeito do tempo de viagem nos vários tipos de deslocações para fazer compras; quanto maior o valor de b, maior é o efeito do tempo de deslocação ou distância (Tij) na probabilidade de uma pessoa fazer compras num determinado centro comercial. - Determina-se o número de clientes, membros da universidade, que farão as suas compras no centro comercial, multiplicando a probabilidade, (1), pelo número de membros da comunidade universitária.
- Faz-se uma previsão do valor total das vendas aos clientes, membros da comunidade universitária, no centro comercial multiplicando o número de clientes, membros da universidade, que farão as suas compras no centro comercial, (2), por uma estimativa do valor médio das vendas a cada um, de cada vez que vai às compras num hipermercado.
Previsão das vendas aos 12 000 membros da comunidade universitária, por centro comercial, supondo que b = 2 e um valor médio de 50 UM gastas de cada vez que cada um faz compras num hipermercado:
Parque
- Pij = (92,90 / 4,828²) / [(92,90 / 4,828²) + (46,45 / 8,047²) + (9,29 / 1,609²)] = 0,48
- 0,48 × 12 000 = 5 760 clientes
- 5 760 × 50 = 288 000 UM
Cascata
- Pij = (46,45 / 8,047²) / [(92,90 / 4,828²) + (46,45 / 8,047²) + (9,29 / 1,609²)] = 0,09
- 0,09 × 12 000 = 1 080 clientes
- 1 080 × 50 = 54 000 UM
Cidadela
- Pij = (9,29 / 1,609²) / [(92,90 / 4,828²) + (46,45 / 8,047²) + (9,29 / 1,609²)] = 1 - 0,48 - 0,09 = 0,43
- 0,43 × 12 000 = (1 - 0,48 - 0,09) × 12 000 = 12 000 - 5 760 - 1 080 = 5 160 clientes
- 5 160 × 50 = (12 000 - 5 760 - 1 080) × 50 = 258 000 UM
ou seja, atendendo a que o total gasto nos hipermercados é 12 000 × 50 = 600 000 UM, então,
Parque: 0,48 × 600 000 = 288 000 UM
Cascata: 0,09 × 600 000 = 54 000 UM
Cidadela: 0,43 × 600 000 = 600 000 - 288 000 - 54 000 = 258 000 UM (Levy e Weitz, 2004 e Prazeres, 2006e).
Localização de Hipermercado em Relação a Áreas Urbanas
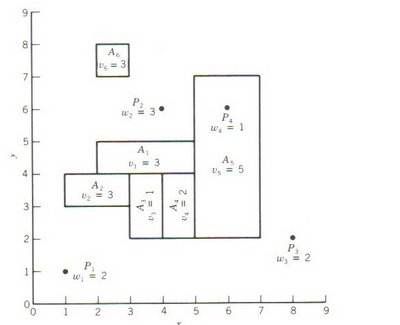
Suponha-se que numa região existem 4 grandes clientes institucionais, representados por pontos na Figura 5.15, e seis áreas habitacionais, representadas na mesma figura. Neste caso, os pesos podem estar associados ao número de entregas a fazer por período de tempo.
(carregar com o cursor na figura para ver em tamanho grande)
Usando a abordagem da força resultante para cada eixo, é possível resolver problemas de localização rectilineares envolvendo localizações em áreas para os elementos existentes, quando as áreas têm formato rectangular e o peso se distribui uniformemente pela área. Uma vez que estas suposições podem ser satisfeitas fazendo os rectângulos suficientemente pequenos, o procedimento gráfico pode ser aplicado a situações envolvendo áreas de forma irregular.
A área habitacional j é designada por Aj e o seu peso associado denotado por vj. O total dos pesos é 25. Representando graficamente o peso cumulativo à direita de x, para 0 ≤ x ≤ 8, na Figura 5.16, verifica-se que metade do peso total é consumida quando x* = 4. Da mesma forma, vê-se na Figura 5.17 que metade do peso é consumida quando y* = 4 1/8. Note-se que a distribuição uniforme do peso por uma área resulta num consumo linear do peso.

(carregar com o cursor na figura para ver em tamanho grande)
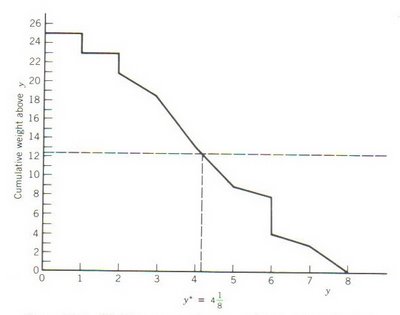
(carregar com o cursor na figura para ver em tamanho grande)
Para exemplificar, movendo de x = 0 para x = 3, passa-se P1, A2, A6 e um terço de A1. Então, foram consumidos w1 + v2 + v6 + (v1 / 3), restando 25 – (2 + 3 + 3 + 1) = 16 como peso cumulativo à direita de x = 3. Da mesma forma, para y = 5 passa-se P1, P3, A1, A2, A3, A4 e três quintos de A5, então, 25 – (2 + 2 + 3 + 3 + 1 + 2 + 3) = 9 é o peso cumulativo acima de y = 5 (Santos, 2006i).


0 Comments:
Post a Comment
<< Home